Chapter 5: Additional Topics

5.1 Polar Coordinates

Introduction

Up to now we have done all our work in this course and previous courses in the Cartesian Coordinate system. This is the square grid where we have an \(x\)-axis and a \(y\)-axis and every point in the plane can be described by using two pieces of information: distance traveled in the \(x\) direction and distance traveled in the \(y\)-direction. The points and their distances from the origin are indicated as an ordered pair \((x, y)\).

Figure 1: Figure 5.1: Point in the plane identified with Cartesian \((x,y)\) and polar \((r, \theta)\) coordinates

While this system of identifying points on the plane is quite useful it is not the only way to do so. Another way is the use of polar coordinates. Polar coordinates are drawn in the plane starting at a fixed point \(O\) called the pole or origin and a ray in the positive \(x\) direction called the polar axis. Polar coordinates also use two pieces of information to identify a point in the plane:

\(\theta\): an angle measured from the polar axis

\(r\): a directed distance from the pole.

Figure 5.1 shows a point in the plane identified with both coordinate systems. In polar coordinates the point is \((r, \theta)\). In Cartesian coordinates it is useful to draw a square grid to measure distances in the \(x\) and \(y\) directions but this grid is not what we need for polar coordinates. In polar coordinates we have concentric circles that represent the radii and lines extending out radially indicating the angles. See Figures 5.2 and 5.3 for two different versions. You can mark the angles in either degrees or radians but radians is the most common. We will primarily use radians for all our work with polar coordinates in this text.

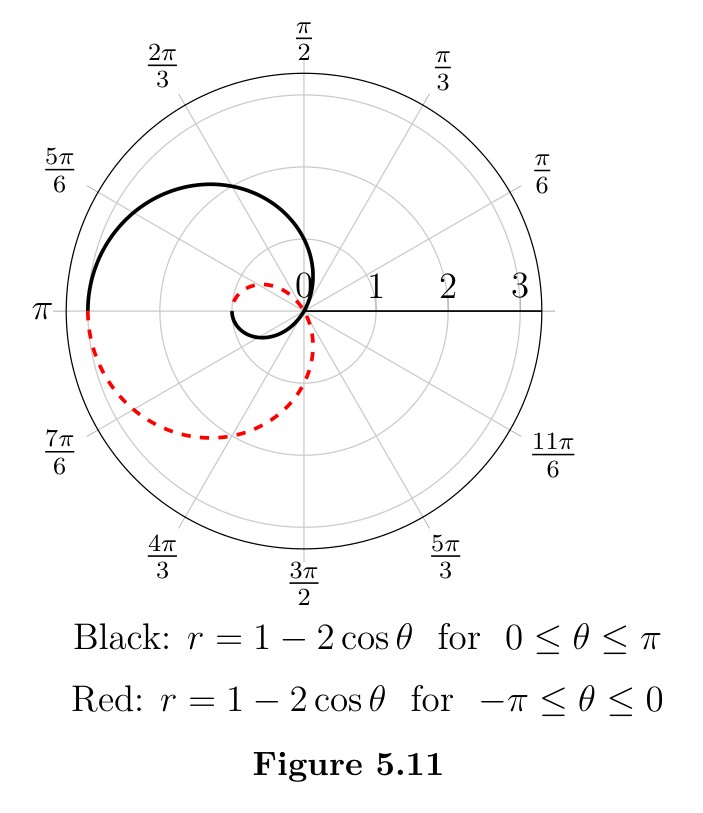
The angle \(\theta\) can be both positive and negative just as when constructing reference angles. When positive, it is measured starting at the polar axis traveling in the counter clockwise direction and, when negative, it is measured in the clockwise direction. The radius \(r\) is called a directed distance because it can also be positive or negative. If it is positive it is measured from the origin in the direction of the angle and if negative it is measured in the opposite direction. See Example 5.1.1.

Figure 2: Figure 5.2: Polar graph paper in degrees

Figure 3: Figure 5.3: Polar graph paper in radians

TipExample 5.1.1

Plot the points \(\left( 1.5, \dfrac{5\pi}{6} \right)\) and \(\left( -1.5, \dfrac{7\pi}{6} \right)\)

Figure 4: Figure 5.4: Plot of polar points

Solution: When graphing in polar coordinates always find the angle first, then the radius. The line that represents the angle passes through the origin and extends indefinitely in both directions. The lines representing the angles in Figure 5.4 are marked with an arrow in the positive direction. If the radius is positive you measure from the center in that direction. If the radius is negative you measure in the opposite direction starting from the center. Just as we could have an infinite number of representation for an angle drawn in standard position there are an infinite number of ways to represent every point in polar coordinates. Notice that if we plot \(\left( 1.5, \dfrac{\pi}{6} \right)\) it is the same point as \(\left( -1.5, \dfrac{7\pi}{6} \right)\).

Converting Between Cartesian and Polar Coordinates

To convert between the coordinate systems we will use a triangle. By drawing a triangle on our previous representation of a point on the plane we can use the trigonometric functions and the Pythagorean theorem to relate \(x\), \(y\), \(r\) and \(\theta\).

NoteConverting Between Polar and Cartesian Coordinates

\(\cos \theta = \dfrac{x}{r}\)	\(x = r \cos \theta\)
\(\sin \theta = \dfrac{y}{r}\)	\(y = r \sin \theta\)
\(\tan \theta = \dfrac{y}{x}\)	\(r^2 = x^2 + y^2\)

Figure 5.5

You need to be careful when calculating \(\theta\) because \(\tan^{-1} \left( \dfrac{y}{x} \right)\) only gives answers between \(-\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}\).

TipExample 5.1.2

Convert the Cartesian points \((1,1)\) and \((-2, 3)\) to polar coordinates.

Figure 5: Figure 5.6: Plot of \((1,1)\)

Figure 6: Figure 5.7: Plot of \((-2,3)\)

Solution: It is often best to plot the point before converting. It will be easier to see if your answer makes sense. Figure 5.6 is the plot of \((1,1)\) and Figure 5.7 is the plot of \((-2, 3)\).

\((x,y) = (1,1)\)	\((x,y) = (-2,3)\)
This is the standard \(45\)-\(45\)-\(90\) triangle so	\(r = \sqrt{2^2+3^2}\)
\(r = \sqrt{2}\) and	\(r = \sqrt{13}\)
\(\theta = \dfrac{\pi}{4}\)	\(\theta' = \tan^{-1}\left( \dfrac{3}{2}\right)\)
	\(\theta = \pi - \theta' = 2.16\)
\(\boxed{(r, \theta) = \left( \sqrt{2}, \dfrac{\pi}{4}\right)}\)	\(\boxed{(r, \theta) = \left( \sqrt{13}, 2.16\right)}\)

TipExample 5.1.3

Convert the polar points \(\left( 7, \dfrac{\pi}{3}\right)\) and \(\left( 7, -\dfrac{5\pi}{3}\right)\) to Cartesian coordinates.

Figure 7: Figure 5.8: Plot of \(\left(7, \frac{\pi}{3}\right)\) and \(\left(7, -\frac{5\pi}{3}\right)\)

Solution: Again we will plot the points before converting. Figure 5.8 is the plot of \(\left( 7, \dfrac{\pi}{3}\right)\) and \(\left( 7, -\dfrac{5\pi}{3}\right)\). These are both the same point so we only have to calculate the Cartesian coordinates for one of them. \[\begin{align*} x &= r \cos \theta & y &= r \sin \theta\\ &= 7 \cos \frac{\pi}{3} & &= 7 \sin \frac{\pi}{3}\\ &= \frac{7}{2} & &= \frac{7\sqrt{3}}{2} \end{align*}\]

\[\boxed{(x, y)= \left(\frac{7}{2}, \frac{7\sqrt{3}}{2} \right)}\]

Converting Between Cartesian and Polar Equations

TipExample 5.1.4

Convert \(r = 2\cos \theta\) to an equation in Cartesian coordinates and identify the shape of the graph.

Solution: The conversion equations are \(x = r \cos \theta\), \(y = r \sin \theta\) and \(r^2 = x^2 + y^2\) so we would like our original equation to have pieces that look like these conversions. Since neither side of our original problem looks exactly like any of our conversion equations we will apply a trick to make it look correct. The trick is to multiply by \(r\) on both sides of the equation and then convert to Cartesian. We will then complete the square to write it in the standard form of a circle. \[\begin{alignat*}{3} r &= 2 \cos \theta &{} \qquad & \text{original equation}\\ r^2 &= 2r \cos \theta &{} \qquad & \text{multiply on both sides by } r\\ x^2 +y^2 &= 2x &{} \qquad & \text{replace } x^2+y^2=r^2 \text{ and } x = r \cos \theta\\ x^2 -2x +y^2 &= 0 &{} \qquad & \text{move all variables to left}\\ x^2 -2x +1 +y^2 &= 1 &{} \qquad & \text{complete the square}\\ (x-1)^2 +y^2 &= 1 &{} \qquad & \text{factor} \end{alignat*}\]

The converted equation is \(\boxed{(x-1)^2 + y^2 = 1}\) which is a circle with center at \((1,0)\) and radius \(1\).

TipExample 5.1.5

Convert \(y = 3x+2\) to a polar equation.

Solution: Here we can use the two conversions \(x = r \cos \theta\) and \(y = r \sin \theta\). We would like to have an equation of the form \(r = f(\theta)\) if possible so we will solve for \(r\). \[\begin{align*} y &= 3x+2\\ r \sin \theta &= 3r \cos \theta+2\\ r \sin \theta - 3r \cos \theta &= 2\\ r (\sin \theta - 3 \cos \theta) &= 2 \end{align*}\]

\[\boxed{r = \dfrac{2}{\sin \theta - 3 \cos \theta}}\]

Graphing Polar Equations

TipExample 5.1.6

Graph the polar equation \(r = \theta\)

Figure 8: Figure 5.9: \(r = \theta\)

Solution: To graph this we will create a table of points by selecting \(\theta\) values and calculating the corresponding \(r\) values. Then we connect the dots with a smooth line traveling in a clockwise direction around the circle (Figure 5.9). A more complicated graph will need more points.

\(\theta\)	\(r\)	\((r, \theta)\)
\(0\)	\(0\)	\((0, 0)\)
\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{4}\)	\(\left(\dfrac{\pi}{4}, \dfrac{\pi}{4}\right)\)
\(\dfrac{\pi}{2}\)	\(\dfrac{\pi}{2}\)	\(\left(\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\)
\(\dfrac{3\pi}{4}\)	\(\dfrac{3\pi}{4}\)	\(\left(\dfrac{3\pi}{4}, \dfrac{3\pi}{4}\right)\)
\(\pi\)	\(\pi\)	\((\pi, \pi)\)
\(\dfrac{5\pi}{4}\)	\(\dfrac{5\pi}{4}\)	\(\left(\dfrac{5\pi}{4}, \dfrac{5\pi}{4}\right)\)
\(\dfrac{3\pi}{2}\)	\(\dfrac{3\pi}{2}\)	\(\left(\dfrac{3\pi}{2}, \dfrac{3\pi}{2}\right)\)

TipExample 5.1.7

Graph the polar equation \(r = 2\cos \theta\).

Figure 9

Solution: To graph this we will create a table of points by selecting \(\theta\) values and calculating the corresponding \(r\) values. Then we connect the dots with a smooth line (Figure 5.10).

\(\theta\)	\(r\)	\((r, \theta)\)
\(0\)	\(2\)	\((2, 0)\)
\(\dfrac{\pi}{6}\)	\(\sqrt{3}\)	\(\left(\dfrac{\pi}{6}, \sqrt{3}\right)\)
\(\dfrac{\pi}{3}\)	\(1\)	\(\left(\dfrac{\pi}{3}, 1\right)\)
\(\dfrac{\pi}{2}\)	\(0\)	\(\left(\dfrac{\pi}{2}, 0\right)\)
\(\dfrac{2\pi}{3}\)	\(-1\)	\(\left(\dfrac{2\pi}{3}, -\sqrt{3}\right)\)
\(\dfrac{5\pi}{6}\)	\(-\sqrt{3}\)	\(\left(\dfrac{5\pi}{6}, -1\right)\)
\(\pi\)	\(-2\)	\((\pi, -2)\)

It is not necessary to plot any more points because any extra points will be repeats of the ones in the table. Notice that this is a circle of radius 1 centered at \((1, 0)\) and this is also what was calculated in Example 5.1.4. It is not always clear how many points you need to get an accurate graph. It is better to have too many points than too few. While most of the polar graphs are symmetric they can have interesting behavior.

TipExample 5.1.8

Graph the polar equation \(r = 1 - 2\cos \theta\).

Solution: To graph this we will create a table of points by selecting \(\theta\) values and calculating the corresponding \(r\) value. We will use symmetry for this because \(\cos \theta = \cos (-\theta)\) so we can plot the values \(0 \leq \theta \leq \pi\) and we have equal values for the negative values \(-\pi \leq \theta \leq 0\). Notice that this graph is symmetric with respect to the polar axis.

\(\theta\)	\(r\)	\((r, \theta)\)
\(0\)	\(-1\)	\((0, -1)\)
\(\dfrac{\pi}{6}\)	\(\approx -0.7321\)	\(\left(\dfrac{\pi}{6}, -0.7321\right)\)
\(\dfrac{\pi}{3}\)	\(0\)	\(\left(\dfrac{\pi}{3}, 0\right)\)
\(\dfrac{\pi}{2}\)	\(1\)	\(\left(\dfrac{\pi}{2}, 1\right)\)
\(\dfrac{2\pi}{3}\)	\(2\)	\(\left(\dfrac{2\pi}{3}, 2\right)\)
\(\dfrac{5\pi}{6}\)	\(\approx 2.7321\)	\(\left(\dfrac{5\pi}{6}, 2.7321\right)\)
\(\pi\)	\(3\)	\((\pi, 3)\)

Then we connect the dots with a smooth line traveling in a clockwise direction around the circle (Figure 5.11). The solid black part of the graph is the table data and the red dashed part of the graph is the part plotted with symmetry.

Figure 10

TipExample 5.1.9

Graph the polar equation \(r = 1 + 2\sin(2\theta)\).

Solution: Since this equation has a \(2\theta\) inside the sine we will use values of \(\theta\) in increments of \(\dfrac{\pi}{12}\) (or \(15^\circ\)) because when we double those we are at multiples of \(\dfrac{\pi}{6}\) (\(30^\circ\)) or \(\dfrac{\pi}{4}\) (\(45^\circ\)). These are the values that will be easier to graph because they are our special angles. We will also start at \(-\dfrac{\pi}{12}\) because that will be a point at the origin. We plot points to \(\dfrac{7\pi}{12}\) because that brings the \(r\) values back to zero. This set of data produces the large lobe in the first quadrant. Continuing to plot points between \(\dfrac{7\pi}{12} \leq \theta \leq \dfrac{11\pi}{12}\) produces the smaller lobe in the fourth quadrant.

\(\theta\)	\(r\)	\((r, \theta)\)
\(-\dfrac{\pi}{12}\)	\(0\)	\(\left(-\dfrac{\pi}{12}, 0\right)\)
\(0\)	\(1\)	\((0, 1)\)
\(\dfrac{\pi}{12}\)	\(2\)	\(\left(\dfrac{\pi}{12}, 2\right)\)
\(\dfrac{\pi}{6}\)	\(2.732\)	\(\left(\dfrac{\pi}{6}, 2.732\right)\)
\(\dfrac{\pi}{4}\)	\(3\)	\(\left(\dfrac{\pi}{4}, 3\right)\)
\(\dfrac{\pi}{3}\)	\(2.732\)	\(\left(\dfrac{\pi}{3}, 2.732\right)\)
\(\dfrac{5\pi}{12}\)	\(2\)	\(\left(\dfrac{5\pi}{12}, 2\right)\)
\(\dfrac{\pi}{2}\)	\(1\)	\(\left(\dfrac{\pi}{2}, 1\right)\)
\(\dfrac{7\pi}{12}\)	\(0\)	\(\left(\dfrac{7\pi}{12}, 0\right)\)
\(\dfrac{3\pi}{4}\)	\(-1\)	\(\left(\dfrac{3\pi}{4}, -1\right)\)
\(\dfrac{11\pi}{12}\)	\(0\)	\(\left(\dfrac{11\pi}{12}, 0\right)\)

Figure 11

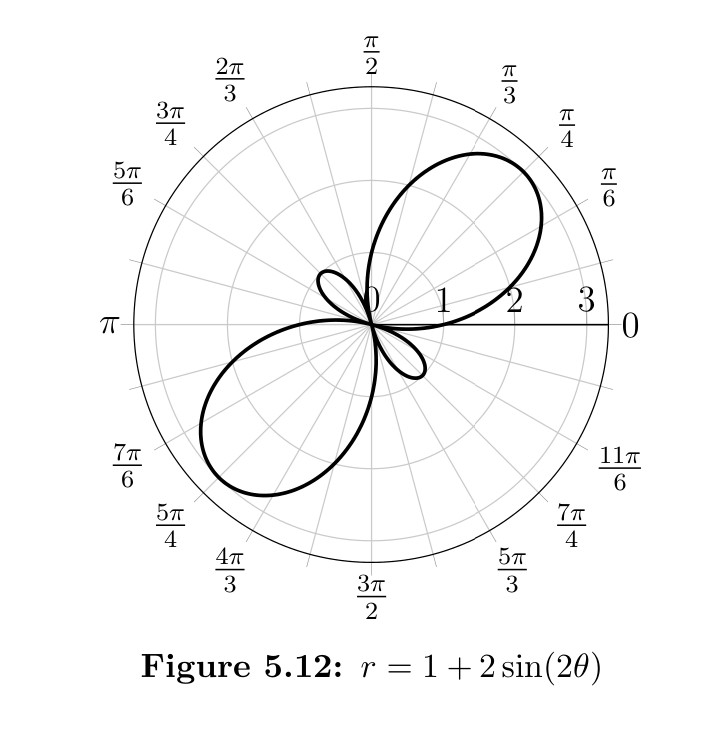
The process of sketching this figure is shown below. The process of sketching the points in order, with a smooth curve, is demonstrated through the 10 diagrams in Figure 5.12.

Figure 12

---

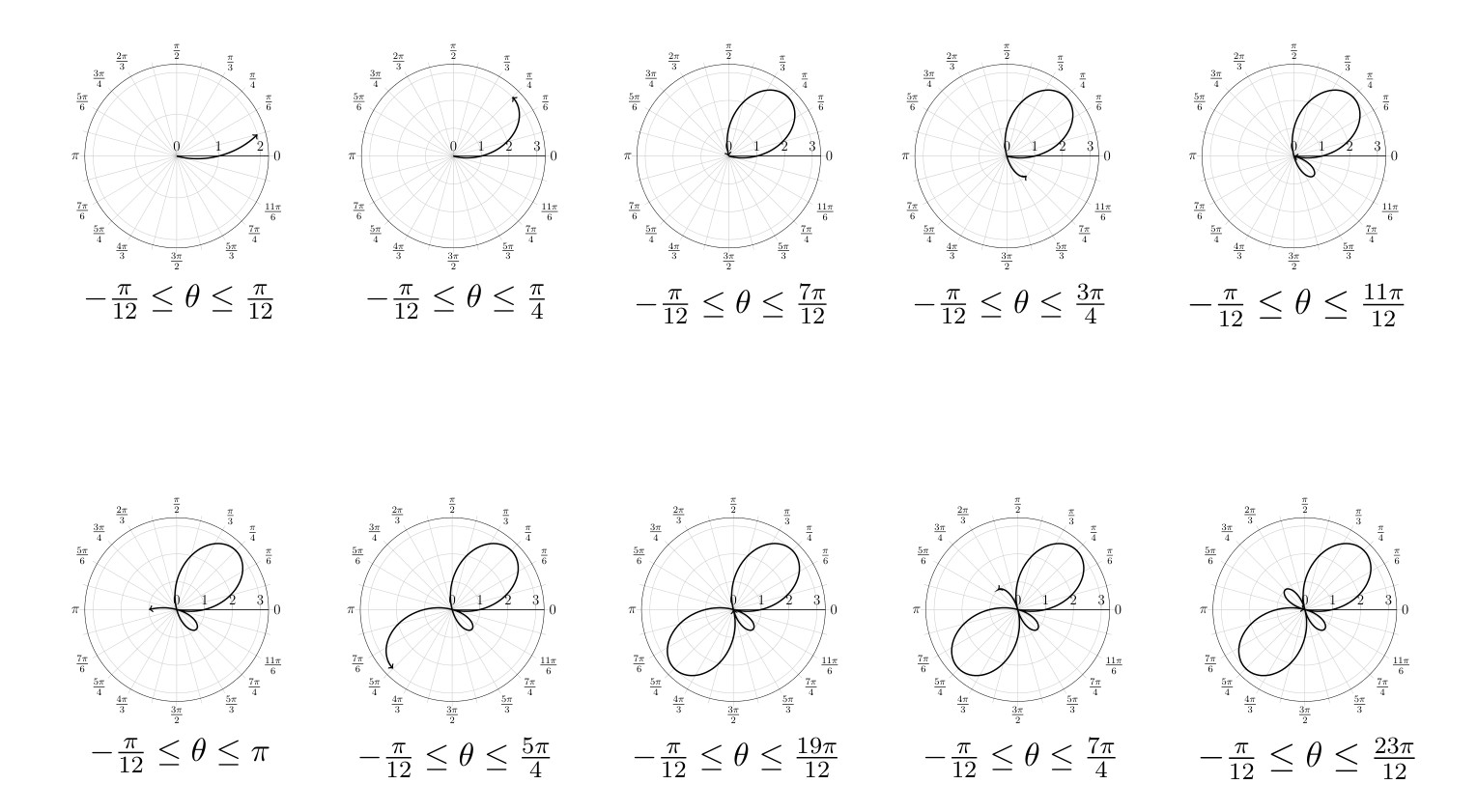
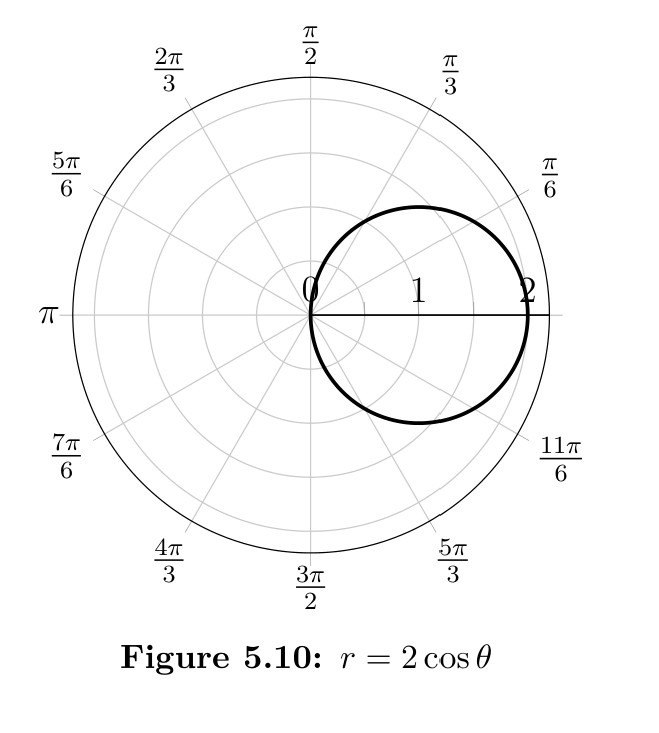
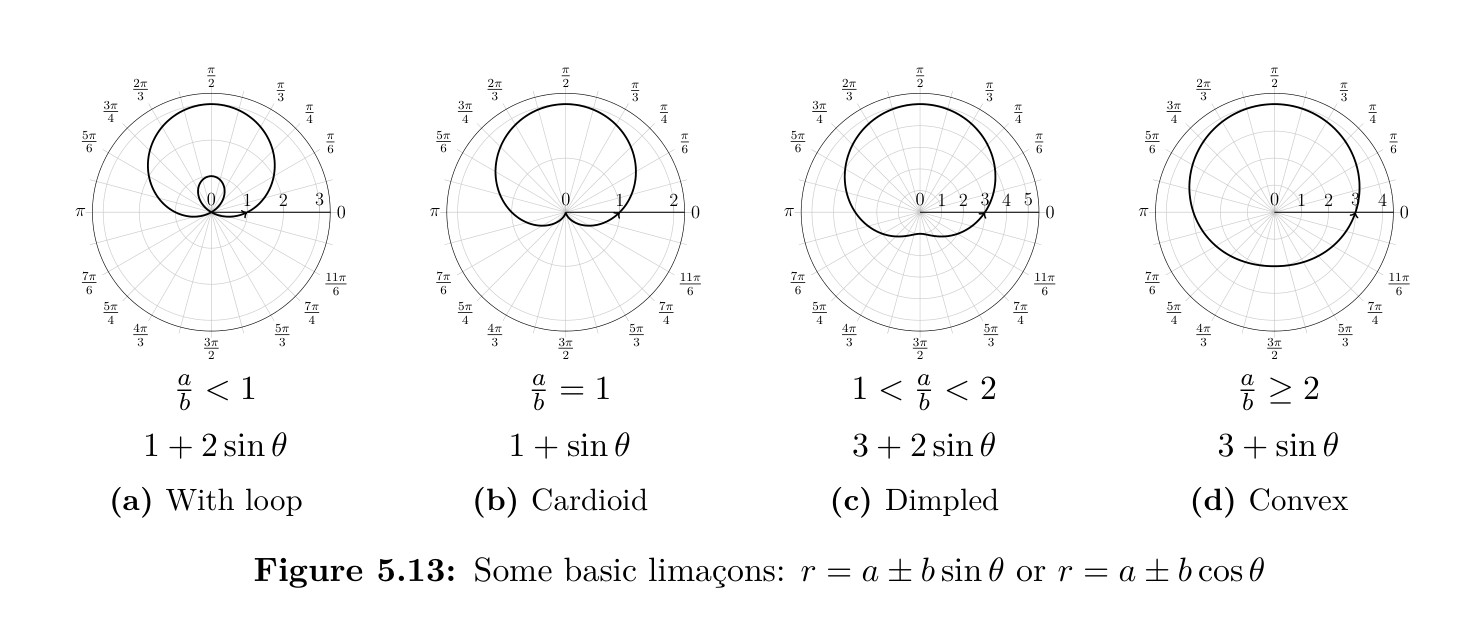
There are some general shapes that the polar graphs can have. The figure drawn in Example 5.1.8 is called a limaçon and is the name given to any curve with an equation of the form \(r=a \pm b \sin \theta\) or \(r=a \pm b \cos \theta\). The limaçon can take on one of four shapes depending on the relationship between \(a\) and \(b\). See Figure 5.13. The limaçon will be symmetric with the vertical axis if it is a sine graph and symmetric with the horizontal if a cosine graph.

Figure 13

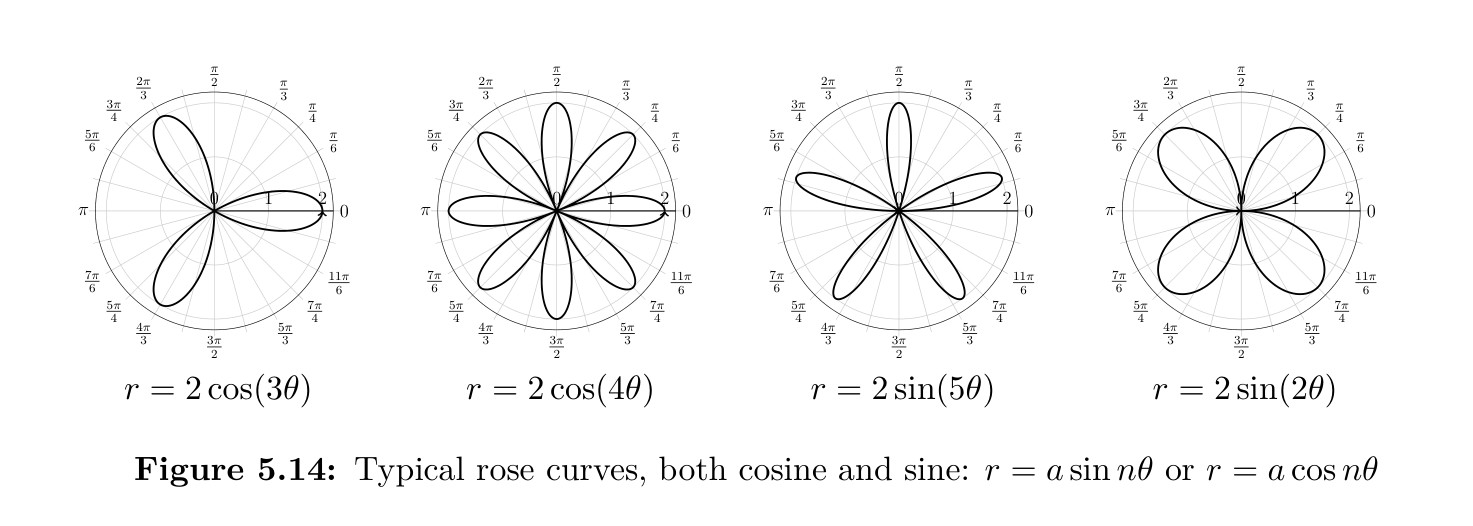
Another typical shape with polar graphs is the rose shape. This was demonstrated in Example 5.1.9. The rose curve comes from equations of the form \(r = a \cos(n\theta)\) or \(r = a \sin(n\theta)\) and the rose has \(n\) petals if \(n\) is odd and has \(2n\) petals if \(n\) is even.

Figure 14

---

5.1 Exercises

For Exercises 1-8, plot the point and convert from polar to Cartesian coordinates.

1. \((4, 210^\circ)\)

2. \(\left(5,\dfrac{7\pi}{6}\right)\)

3. \(\left(5,\dfrac{3\pi}{4}\right)\)

4. \(\left(3,\dfrac{-3\pi}{4}\right)\)

5. \(\left(4,\dfrac{7\pi}{3}\right)\)

6. \(\left(-5,\dfrac{11\pi}{4}\right)\)

7. \(\left(-3,\dfrac{-3\pi}{4}\right)\)

8. \(\left(2, \dfrac{\pi}{2}\right)\)

For Exercises 9-16, convert from Cartesian to polar coordinates.

9. \((6,2)\)

10. \((-1,3)\)

11. \((1,1)\)

12. \((-3,-3)\)

13. \((-7,-1)\)

14. \((1,-\sqrt{3})\)

15. \((-3\sqrt{3},-3)\)

16. \(\left(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}\right)\)

For Exercises 17-22, convert the Cartesian equation to a polar equation.

17. \(y=3\)

18. \(y=x^2\)

19. \(x^2+y^2=9\)

20. \(x^2+y^2 = 9y\)

21. \(y = \sqrt{3}x\)

22. \(5y+x+2=0\)

For Exercises 23-28, convert the polar equation to a Cartesian equation.

23. \(\theta = \dfrac{\pi}{4}\)

24. \(r=4\cos \theta\)

25. \(r = 5\)

26. \(r = -6\sin \theta\)

27. \(r = \dfrac{4}{\sin \theta + 7 \cos \theta}\)

28. \(r = 2\sec \theta\)

For Exercises 29-37, sketch the graph of the polar equation.

29. \(r=4\cos \theta\)

30. \(r = -6\sin (2\theta)\)

31. \(r = 3\sin (5\theta)\)

32. \(r=4+4\cos \theta\)

33. \(r = 1+2\cos (2\theta)\)

34. \(r = 3\cos (3\theta)\)

35. \(r = 5\)

36. \(r = 2 + 4 \sin \theta\)

37. \(\theta = \dfrac{\pi}{4}\)

5.2 Vectors in the Plane

Introduction

We deal with many quantities that are represented by a number that shows their magnitude. These include speed, money, time, length and temperature. Quantities that are represented only by their magnitude or size are called scalars. When you travel in your car and you look at the speedometer it tells you how fast you are going but not where you are going. This is a scalar value and is called the speed.

A vector is a quantity that has both a magnitude (size) and a direction. To describe a vector you must have both parts. If you know that you are traveling at 150 mph north then that would be a vector quantity and it is called the velocity. It tells you how fast you are traveling, speed is 150 mph, as well as the direction, north.

Vector Representations

Figure 15: Figure 5.15: Equivalent vectors: same magnitude and direction

When we write a vector there are two common ways to do it. If we want to talk about “vector \(v\)” we can either write the \(\mathbf{v}\) in bold or write the \(\vec{v}\) with an arrow over it. In this text we will most often use the arrow notation but do be aware that the bold notation is also common.

To describe a vector we need to talk about both the magnitude and direction. The magnitude of a vector is represented by the notation \(||\vec{v}||\). The direction can be described in different ways and depends on the application. For example you might say that a jet is traveling in the direction \(10^\circ\) north of east, or a force is applied at a particular angle or with a particular slope.

A vector can be represented by simply an arrow: in Figure 5.15 the vector \(\vec{v} = \overrightarrow{PQ}\) which starts at point \(P\) and ends at point \(Q\) has magnitude equal to its length (\(||\vec{v}||\)) and direction as indicated. The vector can be moved around in the plane as long as the length and direction are unchanged. All the vectors in Figure 5.15 are equivalent because they all have the same length and point in the same direction. When the vector is drawn this way the length is always the magnitude. An accurate picture is necessary to accurately describe a vector this way. Sometimes it is called a directed line segment.

TipExample 5.2.1

Show that the directed segment \(\vec{u}\) which starts at \(P(-3,-2)\) and ends at \(Q(1,4)\) is equivalent to the directed segment \(\vec{v}\) which starts at \(R(3,1)\) and ends at \(S(7,7)\).

Figure 16: Figure 5.16: Equivalent directed segments

Solution: To show that the two vectors are equivalent we need to show that they have the same length and direction. Using the distance formula we can see they have the same length. \[\begin{align*} ||\vec{u}|| &= \sqrt{(1-(-3))^2+(4-(-2))^2} = \sqrt{4^2+6^2} = 2\sqrt{13}\\ ||\vec{v}|| &= \sqrt{(7-3)^2+(7-1)^2} = \sqrt{4^2+6^2} = 2\sqrt{13} \end{align*}\]

Both of these vectors have the same direction because they are both pointing to the upper right and have the same slope:

\[\frac{\Delta y}{\Delta x} = \frac{(4-(-2))}{(1-(-3))} = \frac{(7-1)}{(7-3)} = \frac{3}{2}\]

Thus they are equivalent.

---

Figure 17: Figure 5.17: A vector split into the \(x\) and \(y\) components

A vector drawn starting at the origin is in standard position as shown in Figure 5.17. A vector in standard position has initial point at the origin \((0,0)\) and can be represented by the endpoint of the vector \((a, b)\). This is known as representing the vector by components: \(\vec{v} = \langle a, b \rangle\). It is common to see this written as \(\vec{v} = \langle v_x, v_y \rangle\). Notice the use of “angle brackets” \(\langle ~ \rangle\) to write the vector. This distinguishes it from the point at the end of the vector. Writing a vector as components is generally preferable because it is easier to perform calculations with components rather than directed line segments. Also, while all the work in this book is with two dimensional vectors you can also write vectors in three or even more dimensions. It is very difficult to draw a directed segment in three dimensions while writing it with components is quite straight forward.

If you want to write \(\vec{v}\) from point \(P\) to point \(Q\) then \(\vec{v} = Q - P\). For example in Example 5.2.1, \(\vec{u} = \overrightarrow{PQ} =(1,4) - (-3,-2) = \langle 4,6 \rangle\). It is important to subtract in the correct order. It is always “end point” minus “starting point”. If you subtract in the wrong order you end up with a vector that has the same length but points in the opposite direction.

NoteComponent Form of a Vector

The component form of a vector \(\vec{v}\) with initial point \(P(p_1, p_2)\) and end point \(Q(q_1, q_2)\) is

\[\overrightarrow{PQ} = \langle q_1 - p_1,\ q_2 - p_2\rangle = \langle v_x, v_y \rangle = \vec{v}\]

The magnitude of \(\vec{v}\), \(||\vec{v}||\), is found by the Pythagorean theorem.

\[||\vec{v}|| = \sqrt{(q_1 - p_1)^2+(q_2 - p_2)^2} = \sqrt{v_x^2+v_y^2}\]

A vector of magnitude (or length) 1 is called a unit vector. To create a unit vector you can divide any vector by its length. A unit vector in the direction of \(\vec{v}\) is given by

\[\text{unit vector in the direction of } \vec{v} = \frac{\vec{v}}{||\vec{v}||}\]

Any vector \(\vec{v}\) can be written as a product of the magnitude and direction, where the direction is the unit vector in the direction of \(\vec{v}\)

\[\vec{v} = ||\vec{v}|| \cdot \frac{\vec{v}}{||\vec{v}||} = \text{magnitude} \cdot \text{direction}\]

TipExample 5.2.2

Find the component form of the vector \(\vec{v}\) that starts at \(P(1,2)\) and ends at \(Q(-3,4)\). Find the length of \(\vec{v}\). Find a unit vector in the direction of \(\vec{v}\). Write \(\vec{v}\) as “magnitude \(\cdot\) direction” where the direction is the unit vector. Sketch the vector in standard position.

Solution:

\[\vec{v} = \langle q_1 - p_1,\ q_2 - p_2\rangle = \langle (-3 - 1),\ (4 - 2) \rangle = \boxed{\vec{v} = \langle -4, 2 \rangle}\]

The length: \(\quad ||\vec{v}|| = \sqrt{v_x^2+v_y^2} =\sqrt{(-4)^2+(2)^2} = \boxed{||\vec{v}|| = 2\sqrt{5}}\)

Unit vector: \(\quad \vec{u} = \dfrac{\vec{v}}{||\vec{v}||} = \dfrac{\langle -4, 2 \rangle}{2\sqrt{5}} = \boxed{\left\langle\dfrac{-2}{\sqrt{5}},\ \dfrac{1}{\sqrt{5}} \right\rangle}\)

“magnitude \(\cdot\) direction”: \(\quad \boxed{\vec{v} = 2\sqrt{5} \cdot \left\langle\dfrac{-2}{\sqrt{5}},\ \dfrac{1}{\sqrt{5}} \right\rangle}\)

Figure 18: Figure 5.18: Vector \(\vec{v}\) from \(P(1,2)\) to \(Q(-3,4)\) in standard position

TipExample 5.2.3

Write the component form of the vector \(\vec{v}\) with magnitude 7 and direction \(\theta = 132^\circ\) measured from the positive \(x\)-axis. Sketch the vector in standard position. Find a unit vector in the direction of \(\vec{v}\). Write \(\vec{v}\) as “magnitude \(\cdot\) direction” where the direction is the unit vector.

Solution: To write the vector in components we need to calculate the two legs of the triangle shown in Figure 5.19. We can do this by using the sine and cosine as shown in Figure 5.17.

\[v_x = ||\vec{v}|| \cos \theta = 7 \cos (132^\circ) = -4.7\]

\[v_y = ||\vec{v}|| \sin \theta = 7 \sin (132^\circ) = 5.2\]

So \(\boxed{\vec{v} = \langle -4.7, 5.2 \rangle}\). Notice that the signs of the trigonometric functions give the correct sign on the components.

Unit vector: \(\quad \vec{u} = \dfrac{\vec{v}}{||\vec{v}||} = \dfrac{\langle -4.7, 5.2 \rangle}{7} = \boxed{\left\langle\dfrac{-4.7}{7},\ \dfrac{5.2}{7} \right\rangle}\)

“magnitude \(\cdot\) direction”: \(\quad \boxed{\vec{v} = 7 \cdot \left\langle\dfrac{-4.7}{7},\ \dfrac{5.2}{7} \right\rangle}\)

Figure 19: Figure 5.19: Vector with magnitude 7 at \(\theta = 132^\circ\)

---

Vector Operations

There are mathematical operations that we can do with vectors. The two most common are multiplication by a scalar and vector addition. Recall that a scalar is a number. If you want to multiply a vector \(\vec{v}\) by a scalar \(k\) there are two ways to think about it. Multiplying by the scalar \(k\) does not change the direction of the vector but makes it longer or shorter by a factor of \(k\). If you have your vector written in components \(\vec{v} = \langle v_x, v_y \rangle\) then each component is multiplied by \(k\):

\[k \cdot \vec{v} = k\cdot \langle v_x, v_y \rangle = \langle k\cdot v_x,\ k\cdot v_y \rangle\]

TipExample 5.2.4

Find the result when \(\vec{u} = \langle 6,-1 \rangle\) is multiplied by 7.

Solution: \(7\vec{u} = 7\langle 6,-1 \rangle = \boxed{\langle 42,-7 \rangle}\)

TipExample 5.2.5

Find the result when \(\vec{u} = \langle 6,-1 \rangle\) is multiplied by \(-1\).

Solution: \((-1)\vec{u} = -\vec{u} = (-1)\langle 6,-1 \rangle = \boxed{\langle -6, 1 \rangle}\)

Note that \(-\vec{u}\) is the same vector as \(\vec{u}\) but pointing in the opposite direction. You can see this if you sketch both on the same set of axes.

---

Adding vectors can be done two ways. We can add vectors that are written as directed line segments or we can add them as components. If you wish to add \(\vec{u}\) to \(\vec{v}\) you draw \(\vec{v}\) and then draw \(\vec{u}\) so that the tail of \(\vec{u}\) starts at the head of \(\vec{v}\). You can see in Figure 5.20 that it does not matter in which order you do this. \(\vec{R} = \vec{u} + \vec{v} = \vec{v} + \vec{u}\)

Figure 20: Figure 5.20: Adding vectors can be done in either order

If the vectors are written as components you can add the \(x\) components and the \(y\) components separately. The component operations are summarized below.

NoteVector Addition and Scalar Multiplication

Given vectors \(\vec{u}=\langle u_x, u_y \rangle\) and \(\vec{v}=\langle v_x, v_y \rangle\) and scalar \(k\), then the sum or difference of \(\vec{u}\) and \(\vec{v}\) is given by

\[\vec{u} + \vec{v}= \langle u_x, u_y \rangle + \langle v_x, v_y \rangle = \langle u_x+ v_x,\ u_y+ v_y \rangle\]

\[\vec{u} - \vec{v}= \langle u_x, u_y \rangle - \langle v_x, v_y \rangle = \langle u_x- v_x,\ u_y- v_y \rangle\]

The scalar multiple of \(k\) and \(\vec{v}\) is

\[k \cdot \vec{v} = k\cdot \langle v_x, v_y \rangle = \langle k\cdot v_x,\ k\cdot v_y \rangle\]

TipExample 5.2.6

Let \(\vec{u} = \langle 1, -2 \rangle\) and \(\vec{v} = \langle -4, 2 \rangle\), and find

1. \(3\vec{u}+\vec{v}\)
2. \(\vec{u}-\vec{v}\)
3. \(\vec{v}-2\vec{u}\)

Solution: To add these we need to add the corresponding components. The order of operations is still valid here — perform the scalar multiplication first and then the vector addition.

1. \(3\vec{u}+\vec{v} = 3\langle 1, -2 \rangle + \langle -4, 2 \rangle = \langle 3, -6 \rangle + \langle -4, 2 \rangle = \boxed{\langle -1, -4 \rangle}\)

The solution is also shown in Figure 5.21 (a).

2. \(\vec{u}-\vec{v} = \langle 1, -2 \rangle - \langle -4, 2 \rangle = \boxed{\langle 5, -4 \rangle}\)

To do this with arrows on paper it is easiest to draw \(-\vec{v}\) and then add that to \(\vec{u}\). Remember that \(-\vec{v}\) is the same as \(\vec{v}\) but the arrow is on the other end of the vector. The solution is shown in Figure 5.21 (b). Notice that we can add in either order; the dotted vectors are the result of \(-\vec{v}+\vec{u}\).

3. \(\vec{v}-2\vec{u}= \langle -4, 2 \rangle - 2\langle 1, -2 \rangle = \langle -4, 2 \rangle + \langle -2, 4 \rangle = \boxed{\langle -6, 6 \rangle}\)

Be careful with the sign when multiplying by the \(-2\). The solution is shown in Figure 5.21 (c). Notice that we can add in either order; the dotted vectors are the result of \(-2\vec{u}+\vec{v}\).

Figure 21: Figure 5.21: Vector addition results for (a), (b), and (c)

TipExample 5.2.7

To avoid a storm a jet travels \(20^\circ\) north of east from Winnipeg for 300 km and then turns to a heading \(62^\circ\) south of east for 1150 km to arrive at Chicago. Find the displacement from Winnipeg to Chicago.

Solution: Figure 5.22 shows the flight path. It is a good idea to draw a picture if possible. While it would be possible to try and measure the vectors and angles it will be easier to add these by components. We will calculate the components for each leg of the journey and then add them up.

Figure 22: Figure 5.22: Flight path from Winnipeg to Chicago

For the first leg \(\overrightarrow{L1} = \langle L1_x, L1_y \rangle\): \[L1_x = 300 \cos (20^\circ) = 282 \qquad L1_y = 300 \sin (20^\circ) = 103\]

For the second leg \(\overrightarrow{L2} = \langle L2_x, L2_y \rangle\): \[L2_x = 1150 \cos (62^\circ) = 540 \qquad L2_y = -1150 \sin (62^\circ) = -1015\]

It is important to notice that the \(y\) component is negative because it points in the negative \(y\) direction. The picture will help make sure the signs are correct on your components.

The resultant vector is

\[\overrightarrow{L1} + \overrightarrow{L2} = \langle 282, 103 \rangle + \langle 540, -1015 \rangle = \langle 822, -912 \rangle\]

The distance from Winnipeg to Chicago is the magnitude of the resultant vector. So the displacement is \(\sqrt{822^2 + (-912)^2} = \boxed{1228 \text{ km}}\).

TipExample 5.2.8

An airplane is traveling with a ground speed of 750 km/hr at a bearing \(37^\circ\) west of north when it encounters a strong wind with a velocity 100 km/hr at a bearing of \(60^\circ\) north of east. Find the resultant speed and direction of the airplane. (Figure 5.23)

Figure 23

Solution: The resultant speed and direction of the airplane (\(\vec{R}\)) is the sum of the plane’s ground speed velocity vector and the wind speed vector. Figure 5.23 shows the relationship between the vectors. To add them we will first write them as components. Let \(\vec{P} = \langle P_x, P_y \rangle\) be the airplane ground speed vector and \(\vec{W} = \langle W_x, W_y \rangle\) be the wind speed vector. \[\begin{align*} \vec{P} &= 750 \langle\cos (127^\circ),\ \sin(127^\circ) \rangle \approx \langle -451, 599 \rangle \text{ km/hr}\\ \vec{W} &= 100 \langle\cos (60^\circ),\ \sin(60^\circ) \rangle \approx \langle 50, 87 \rangle \text{ km/hr} \end{align*}\]

Note the signs on the components of the vectors and compare them to the figure. You expect the \(x\) component of the airplane’s ground speed vector to be negative, and it is.

So the velocity of the plane in the wind is \[\begin{align*} \vec{R} &= \vec{P} + \vec{W} \approx \langle -451, 599 \rangle + \langle 50, 87 \rangle \approx \langle -401, 686 \rangle \text{ km/hr} \end{align*}\]

and the resultant speed of the airplane

\[||\vec{R}|| \approx \sqrt{(-401)^2+(686)^2} \approx 795 \text{ km/hr}\]

For the bearing we will use the angle \(\theta\) made with the negative \(x\)-axis as shown in the figure.

\[\theta = \tan^{-1} \left( \frac{686}{401} \right) \approx 59.7^\circ\]

which we write as \(59.7^\circ\) north of west. The airplane is traveling at \(\boxed{795 \text{ km/hr bearing } 59.7^\circ \text{ north of west}}\).

TipExample 5.2.9

A common use for vectors in physics and engineering applications is adding up forces acting on an object. Suppose there are three forces acting on an object as shown in Figure 5.24: a 40 Newton¹ force acting at \(30^\circ\), a 30 Newton force acting at \(300^\circ\) and a 50 Newton force acting at \(135^\circ\). Find the resultant force vector acting on the object.

Figure 24: Figure 5.24: Three forces acting on an object

Solution: The resultant force will be the sum of all the vectors. To add them we will first write them as components. Since we are measuring all the angles from the horizontal \(x\)-axis the signs of each of the components will be correct because the sine and cosine functions will be positive and negative in the correct quadrants. You can verify this by noticing that the \(x\) component of \(\vec{F}_2\) and the \(y\) component of \(\vec{F}_3\) are both negative. \[\begin{align*} \vec{F}_1 &= 40 \langle\cos (30^\circ),\ \sin(30^\circ) \rangle \approx \langle 34.641, 20 \rangle \text{ N}\\ \vec{F}_2 &= 50 \langle\cos (135^\circ),\ \sin(135^\circ) \rangle \approx \langle -35.355, 35.355 \rangle \text{ N}\\ \vec{F}_3 &= 30 \langle\cos (300^\circ),\ \sin(300^\circ) \rangle \approx \langle 15, -25.981 \rangle \text{ N} \end{align*}\]

\[\vec{R} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 = \langle 34.641, 20 \rangle + \langle -35.355, 35.355 \rangle + \langle 15, -25.981 \rangle\]

\[\boxed{\vec{R} = \langle 14.286, 29.375 \rangle}\]

We can find the magnitude

\[||\vec{R}|| = \sqrt{14.286^2 + 29.375^2} \approx 32.664 \text{ N}\]

and direction of the resultant vector:

\[\theta = \tan^{-1} \left( \frac{29.375}{14.286}\right) \approx 64^\circ\]

---

5.2 Exercises

For Exercises 1-2, write the vector shown in component form.

1. 

2. 

For Exercises 3-4, given the vectors shown, sketch \(\vec{u}+\vec{v}\), \(\vec{u}-\vec{v}\), and \(2\vec{u}\).

3. 

4. 

For Exercises 5-10, write the vector \(\vec{v} = \overrightarrow{PQ}\) in the form \(\vec{v} =\) (magnitude) \(\cdot\) (direction) where the direction is a unit vector. See Example 5.2.2.

5. \(P=(1,2)\), \(Q=(-2,3)\)

6. \(P=(-3,2)\), \(Q=(-3,3)\)

7. \(P=(0,1)\), \(Q=(-2,-7)\)

8. \(P=(-40,23)\), \(Q=(5, -5)\)

9. \(P=(-4,2)\), \(Q=(2, -3)\)

10. \(P=(1,2)\), \(Q=(0,0)\)

For Exercises 11-14, write the vector in component form from the given magnitude and direction.

11. Magnitude: 6; direction: \(30^\circ\)

12. Magnitude: 7; direction: \(120^\circ\)

13. Magnitude: 8; direction: \(225^\circ\)

14. Magnitude: 9; direction: \(330^\circ\)

For Exercises 15-18, given the vectors, compute \(3\vec{u}\), \(2\vec{u}+\vec{v}\), and \(\vec{u}-3\vec{v}\).

15. \(\vec{u} = \langle 2, -2 \rangle\), \(\vec{v} = \langle 3, 2 \rangle\)

16. \(\vec{u} = \langle 1, -2 \rangle\), \(\vec{v} = \langle -4, 2 \rangle\)

17. \(\vec{u} = \langle 2, -3 \rangle\), \(\vec{v} = \langle 1, 2 \rangle\)

18. \(\vec{u} = \langle 3, 4 \rangle\), \(\vec{v} = \langle 5, -6 \rangle\)

19. A woman leaves home and walks 3 miles west, then 2 miles southwest. How far from home is she, and in what direction must she walk to head directly home?

20. A boat leaves the marina and sails 6 miles north, then 2 miles northeast. How far from the marina is the boat, and in what direction must it sail to head directly back to the marina?

21. A person starts walking from home and walks 4 miles east, 2 miles southeast, 5 miles south, 4 miles southwest, and 2 miles east. How far have they walked? If they walked straight home, how far would they have to walk?

22. A person starts walking from home and walks 4 miles east, 7 miles southeast, 6 miles north, 5 miles southwest, and 3 miles east. How far have they walked? If they walked straight home, how far would they have to walk?

23. Three forces act on an object: \(\vec{F}_1 = \langle 2, 5\rangle\), \(\vec{F}_2 = \langle 8, 3\rangle\) and \(\vec{F}_3 = \langle 0, -7\rangle\). Find the net force acting on the object.

24. Three forces act on an object: \(\vec{F}_1 = \langle -2, 5\rangle\), \(\vec{F}_2 = \langle -8, -3\rangle\) and \(\vec{F}_3 = \langle 5, 0\rangle\). Find the net force acting on the object.

25. Suppose there are three forces acting on an object: a 10 Newton force acting at \(45^\circ\), a 20 Newton force acting at \(210^\circ\) and a 15 Newton force acting at \(315^\circ\). Find the resultant force vector acting on the object.

26. A person starts walking from home and walks 6 miles at \(40^\circ\) north of east, then 2 miles at \(15^\circ\) east of south, then 5 miles at \(30^\circ\) south of west. If they walked straight home, how far would they have to walk, and in what direction?

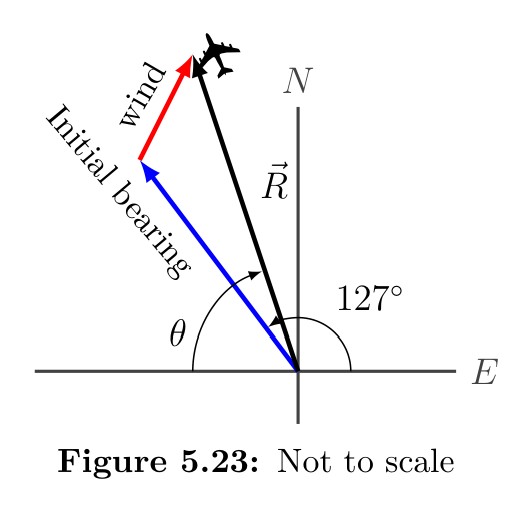
27. An airplane is heading north at an airspeed of 600 km/hr, but there is a wind blowing from the southwest at 80 km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?

28. An airplane is heading north at an airspeed of 500 km/hr, but there is a wind blowing from the northwest at 50 km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?

29. An airplane needs to head due north, but there is a wind blowing from the southwest at 60 km/hr. The plane flies with an airspeed of 550 km/hr. To end up flying due north, the pilot will need to fly the plane how many degrees west of north?

30. An airplane needs to head due north, but there is a wind blowing from the northwest at 80 km/hr. The plane flies with an airspeed of 500 km/hr. To end up flying due north, the pilot will need to fly the plane how many degrees west of north?

31. As part of a video game, the point \(\langle 5, 7 \rangle\) is rotated counterclockwise about the origin through an angle of 35 degrees. Find the new coordinates of this point.

32. As part of a video game, the vector \(\langle 7, 3 \rangle\) is rotated counterclockwise about the origin through an angle of 40 degrees. Find the new coordinates of this point.

Footnotes

1. A Newton (N) is a metric unit of force \(\text{N} = \frac{\text{kg} \cdot \text{m}}{\text{s}^2}\)