Chapter 4: General Triangles

4.1 Law of Sines

Introduction

Up to now all the triangles we have looked at have been right triangles (one angle of 90°). If we knew two other pieces of information about the triangle, lengths of sides or angle measure, we could solve the triangle. Recall that to solve a triangle we wanted to find the lengths of all the sides and the measure of all the angles. Suppose we have a triangle with no right angles such as \(\triangle ABC\) in Figure 4.1. A triangle with no right angles is called an oblique triangle. For our oblique triangle we label the angles with upper case letters \(A\), \(B\), and \(C\) and the sides opposite those angles with the corresponding lower case letter.

Figure 1

Figure 4.1: Oblique triangle

Suppose we want to find a relationship between the \(\sin A\) and the sides of triangle. We can’t use our usual relationship of opposite over hypotenuse because that applies to right triangles. We will draw the height of the triangle \(h\), (in this case from \(B\)), and divide the triangle into two right triangles. With the right triangles we can use our usual relationships:

\[\sin A = \frac{h}{c} \qquad \sin C = \frac{h}{a}\]

Solving each of the equations for \(h\) gives us

\[h = c \sin A \qquad h = a \sin C\]

Setting them equal \[\begin{align*} h &= h \\ c \sin A &= a \sin C\\ \frac{\sin A}{a} &= \frac{\sin C}{c} \end{align*}\]

We can similarly find a relationship for \(\sin B\).

\[\frac{\sin A}{a} = \frac{\sin B}{b}\]

This is known as the Law of Sines and is summarized in the table below.

NoteLaw of Sines

If a triangle has sides of lengths \(a\), \(b\), and \(c\) opposite the angles \(A\), \(B\), and \(C\), respectively, then

\[\frac{\sin A}{a} = \frac{\sin B}{b} =\frac{\sin C}{c}\]

The reciprocal is also true

\[\frac{a}{\sin A} = \frac{b}{\sin B} =\frac{c}{\sin C}\]

Note: The law of sines was proved for an acute triangle where all the angles were less than 90° but the law holds for all triangles.

There are 2 cases where we can use the law of sines. In each of these cases we need three pieces of information.

Case 1:	One side and two angles (AAS or ASA)
Case 2:	Two sides and an angle opposite one of them (Side Side Angle SSA)

TipExample 4.1.1

Case 1: One side and two angles (AAS)

Solve the triangle in Figure 4.2 where \(B = 105^\circ\), \(C = 40^\circ\), and \(b = 20\) meters.

Figure 2: Figure 4.2: Triangle for Example 4.1.1

Solution: Recall that to solve the triangle we need to find the remaining sides and angles. We begin with the missing angle because the sum of the angles of a triangle is always \(180^\circ\). \[\begin{align*} A &= 180 - B - C\\ &= 180 - 105^\circ - 40^\circ\\ &= 35^\circ \end{align*}\]

So \(\boxed{A=35^\circ}\) and by the law of sines we can find the missing sides:

\[\frac{a}{\sin A} = \frac{b}{\sin B} =\frac{c}{\sin C}\]

\[\frac{a}{\sin 35^\circ} = \frac{20}{\sin 105^\circ} =\frac{c}{\sin 40^\circ}\]

So we have the following two equations:

\[\frac{a}{\sin 35^\circ} = \frac{20}{\sin 105^\circ} \qquad \text{and} \qquad \frac{20}{\sin 105^\circ}=\frac{c}{\sin 40^\circ}\]

and we can solve for \(a\) and \(c\)

\[a = \left(\frac{20}{\sin 105^\circ} \right) (\sin 35^\circ) \qquad \text{and} \qquad c = \left(\frac{20}{\sin 105^\circ} \right)(\sin 40^\circ)\]

\[\boxed{a \approx 11.88 \text{ m}} \qquad \text{and} \qquad \boxed{c \approx 13.11 \text{ m}}\]

The Ambiguous Case (SSA)

In Example 4.1.1 we knew two of the angles and one side. This amount of information determines one unique triangle. In the case where you know two sides and an angle opposite one of them there are 3 possible outcomes which are shown in Figure 4.3: no solutions, one solution or two solutions. This is called the ambiguous case.

Figure 3

Figure 4.3: The Ambiguous Cases (SSA): Conditions and Possible Triangles

TipExample 4.1.2

Case 2: Two sides and one angle, two solutions (SSA)

Solve the triangle where \(A = 60^\circ\), \(a=9\), and \(c = 10\).

Figure 4

Figure 4.4: Triangle with two possible solutions

Solution: When you have an angle and two sides you want to draw what you know and then calculate the height. The height will let you know if you can make a triangle or not. The side opposite the angle you know has to be at least as long as the height or you can’t make a triangle.

\[\sin 60^\circ = \frac{h}{10} \implies h = 8.66\]

In Figure 4.4 the red sides are the two possibilities because

\[(h=8.66) < (a = 9) < (c = 10)\]

We start by solving the triangle where \(C\) is an acute angle. Using the law of sines, \(\frac{\sin A}{a} = \frac{\sin C}{c}\), we can solve for \(C\)

\[\frac{\sin 60^\circ}{9} = \frac{\sin C}{10} \implies C = \sin^{-1}\left( \frac{10 \sin 60^\circ}{9} \right) = 74.21^\circ\]

and \(B = 180^\circ - 60^\circ - 74.21^\circ = 45.79^\circ\). Then the final side can be found with the law of sines again.

\[\frac{9}{\sin 60^\circ} = \frac{b}{\sin (45.79^\circ)} \implies b = \frac{9 \sin (45.79^\circ)}{\sin 60^\circ} = 7.45\]

The solution to the first triangle is \(\boxed{C= 74.21^\circ, \ B = 45.79^\circ \text{ and } b = 7.45}\).

The second triangle has \(C' > 90^\circ\) and is the supplementary to \(C\). (Why?)

\[C' = 180^\circ - 74.21^\circ = 105.79^\circ\]

and \(B'= 180^\circ - 60^\circ - 105.79^\circ = 14.21^\circ\). The final side can once again be calculated using the law of sines.

\[\frac{9}{\sin 60^\circ} = \frac{b'}{\sin (14.21^\circ)} \implies b' = \frac{9 \sin (14.21^\circ)}{\sin 60^\circ} = 2.55\]

The solution to the second triangle is \(\boxed{C= 105.79^\circ, \ B = 14.21^\circ \text{ and } b = 2.55}\).

TipExample 4.1.3

Case 3: Two sides and one angle, No solution (SSA)

Solve the triangle where \(A = 30^\circ\), \(a=6\), and \(b = 12.8\).

Figure 5

Figure 4.5: No solution case

Solution: In this case we have no solution because the sides can’t meet. Drawing a diagram of the information you know will help to see this as in Figure 4.5. Consider the height \(h\) of the this possible triangle.

\[\sin 30^\circ = \frac{h}{12.8} \implies h = 6.4\]

Since the height is 6.4 but the side opposite \(A\) has length \(6\), there is no way to construct this triangle and hence there is \(\boxed{\text{no solution}}\).

TipExample 4.1.4

Two radar stations located 10 km apart both detect a UFO located between them. The angle of elevation measured by the first station (\(A\)) is \(36^\circ\) and the angle of elevation measured by the second station (\(C\)) is \(20^\circ\). What is the altitude (\(h\)) of the UFO? See Figure 4.6

Figure 6

Figure 4.6: UFO and radar stations

Solution: The triangle formed by the radar stations and the UFO is not a right triangle. If we call the angle at the UFO \(B\) then we can see that \(B = 180^\circ -36^\circ-20^\circ =124^\circ\). To find the altitude we would need to know one side of a right triangle. Since the height \(h\) makes two right triangles we can use either side \(a\) or \(c\) to solve the problem. We will use side \(a\) but you can verify that you arrive at the same answer if you use side \(c\).

Since we do not have a right triangle and this situation is AAS we will use the law of sines and we know we have only one possible solution.

\[\frac{10{,}000}{\sin 124^\circ} = \frac{a}{\sin 36^\circ} \implies a = \frac{10{,}000 \sin 36^\circ}{\sin 124^\circ} = 7090 \text{ m}\]

Now we can use the standard relationship for the sine to calculate the height.

\[\sin 20^\circ = \frac{h}{a}\]

\[\sin 20^\circ = \frac{h}{7089}\]

\[\boxed{h = 2425 \text{ m}}\]

TipExample 4.1.5

A person standing \(400\) ft from the base of a mountain measures the angle of elevation from the ground to the top of the mountain to be \(25^\circ\). She then walks \(500\) ft straight back and measures the angle of elevation to now be \(20^\circ\). How tall is the mountain?

Solution: This is the same problem (Example 1.5.6) that we had when were were looking at applications of trigonometric functions in Section 1.5. In that problem we used the tangent function and a bit of algebra to do the calculation. This time we will use the law of sines.

Once again we assume that the ground is flat and not inclined relative to the base of the mountain and we let \(h\) be the height of the mountain as in the picture on the right. To use the law of sines we will use the following simplified triangle.

We know that angle \(B\) is supplementary to \(25^\circ\) so \(B= 180^\circ -25^\circ = 155^\circ\). The angles in a triangle add up to \(180^\circ\) so \(C = 5^\circ\). Now we have enough information to use the law of sines to calculate the distance from the second observation point to the top of the mountain, length \(b\) in the diagram.

\[\frac{b}{\sin 155^\circ} = \frac{500}{\sin 5^\circ}\]

\[b = \frac{500\sin 155^\circ}{\sin 5^\circ}\]

\[b \approx 2424 \text{ ft}\]

Now we can use the right triangle with the height \(h\) as the opposite side to the \(20^\circ\) and \(b = 2424\) ft as the hypotenuse.

\[h = 2424 \sin 20^\circ = \boxed{829 \text{ ft}}\]

This is the same height we had calculated earlier but the calculations were simpler.

---

4.1 Exercises

For Exercises 1-6, use the law of sines to solve the triangle \(\triangle ABC\).

1. 

2. 

3. 

4. 

5. 

6. 

For Exercises 7-16, use the law of sines to solve the triangle \(\triangle ABC\). If there is more than one possible solution, give both. If there is no answer state that there is no possible triangle.

7. \(a = 10\), \(A=35^\circ\), \(B = 25^\circ\)

8. \(b = 40\), \(B = 75^\circ\), \(c = 35\)

9. \(A = 40^\circ\), \(B = 45^\circ\), \(c = 15\)

10. \(a = 5\), \(A = 42^\circ\), \(b = 7\)

11. \(a = 40\), \(A = 25^\circ\), \(c = 30\)

12. \(a = 5\), \(A = 47^\circ\), \(b = 9\)

13. \(a = 12\), \(A = 94^\circ\), \(b = 5\)

14. \(a = 12\), \(A = 94^\circ\), \(b = 15\)

15. \(a = 12.3\), \(A = 41^\circ\), \(b = 15.6\)

16. \(a = 22\), \(A = 50^\circ\), \(c = 27\)

For Exercises 17-19, solve for the unknown quantity in Figure 4.7. (Not to scale)

Figure 7: Figure 4.7: UFO and radar stations

17. Two radar stations located \(b=17\) km apart both detect a UFO located between them. The angle of elevation measured by the first station (\(A\)) is \(\alpha = 72^\circ\) and the angle of elevation measured by the second station (\(C\)) is \(\gamma = 51^\circ\). What is the altitude (\(h\)) of the UFO?

18. Two radar stations located \(b=17\) km apart both detect a UFO located between them. The angle of elevation measured by the first station (\(A\)) is \(\alpha = 19^\circ\) and the angle of elevation measured by the second station (\(C\)) is \(\gamma = 151^\circ\). What is the altitude (\(h\)) of the UFO? (Note: The UFO is to the right of station \(C\).)

19. Two radar stations located \(b=107\) km apart both detect a UFO located between them. The angle of elevation measured by the first station (\(A\)) is \(\alpha = 52^\circ\) and the angle of elevation measured by the second station (\(C\)) is \(\gamma = 32^\circ\). What is the altitude (\(h\)) of the UFO?

For Exercises 20-23, solve for the height of the mountain in Figure 4.8. (Not to scale)

Figure 8: Figure 4.8: Mountain height

20. \(\alpha = 31^\circ\), \(\beta = 87^\circ\), \(a=10\) km, \(b=1\) km

21. \(\alpha = 68^\circ\), \(\beta = 71^\circ\), \(a=1000\) m, \(b=250\) m

22. \(\alpha = 37^\circ\), \(\beta = 50^\circ\), \(a=2.5\) km, \(b=2\) km

23. \(\alpha = 50^\circ\), \(\beta = 57^\circ\), \(a=5.0\) km, \(b=50\) km

4.2 Law of Cosines

Introduction

In Section Section 1 we were able to solve triangles with no right angles using the law of sines.

\[\frac{\sin A}{a} = \frac{\sin B}{b} =\frac{\sin C}{c}\]

The law of sines works in two cases:

Case 1:	One side and two angles (AAS or ASA)
Case 2:	Two sides and an angle opposite one of them (SSA)

There are two cases for which the law of sines does not work because we only have one piece of information in each of our ratios. To use the law of sines you have to have all the information to evaluate one of the fractions, an angle and its opposite side, and that is not true for these last two cases.

Case 3:	Three sides (SSS)
Case 4:	Two sides and the included angle (SAS)

Figure 9

Figure 4.9: Law of Cosines diagram

To find another equation to solve the last two cases we will once again construct an oblique triangle and label the angles with upper case letters \(A\), \(B\), and \(C\) and the sides opposite those angles with the corresponding lower case letter. We draw the height of the triangle \(h\), (in this case from \(B\)), and divide the triangle into two right triangles. Now side \(b\) is divided into two pieces, one with length \(x\) and the other with length \(b-x\). Using the Pythagorean theorem we can write an equation for \(h\) for both triangles.

For the triangle on the right

\[h^2 = a^2 - x^2 \tag{1}\]

For the triangle on the left \[\begin{align*} h^2 &= c^2 - (b-x)^2 \\ h^2 &= c^2 - \left( b^2 - 2bx + x^2 \right) \\ \end{align*}\]

\[h^2 = c^2 - b^2 + 2bx - x^2 \tag{2}\]

Both of these equations involve \(x\) but we would like to use only the sides and angles originally given so using the cosine we see that \(x = a \cos C\). Now set equation Equation 1 equal to equation Equation 2 and simplify. \[\begin{align*} h^2 &= h^2\\ a^2 - x^2 &= c^2 - b^2 + 2bx - x^2 \\ c^2 &= a^2 + b^2 -2bx \end{align*}\]

Replace \(x = a \cos C\)

\[c^2 = a^2 + b^2 -2ab \cos C \tag{3}\]

This is known as the Law of Cosines and it relates the three sides of the triangle and one of the angles. This equation can be written in terms of any of the angles. The results are summarized here.

NoteLaw of Cosines

If a triangle has sides of lengths \(a\), \(b\), and \(c\) opposite the angles \(A\), \(B\), and \(C\), respectively, then

Standard Form	Alternative Form
\(a^2 = b^2 + c^2 -2bc \cos A\)	\(\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}\)
\(b^2 = a^2 + c^2 -2ac \cos B\)	\(\cos B = \dfrac{a^2 + c^2 - b^2}{2ac}\)
\(c^2 = a^2 + b^2 -2ab \cos C\)	\(\cos C = \dfrac{a^2 + b^2 - c^2}{2ab}\)

Note: The law of cosines was proved for an acute triangle where all the angles were less than 90° but the law holds for all triangles.

TipExample 4.2.1

Case 3: Three sides (SSS)

Solve the triangle in Figure 4.10 where \(a = 3\), \(b = 9\), and \(c = 8\).

Figure 10

Figure 4.10: Triangle with three sides given

Solution: Recall that to solve the triangle we need to find all sides and angles. We have three sides so we can’t use the law of sines but we can use the law of cosines. We will use the alternate form so we can find one of the angles. We will start with the largest angle, which is opposite the longest side, \(\angle B\). \[\begin{align*} \cos B &= \dfrac{a^2 + c^2 - b^2}{2ac}\\ &= \dfrac{8^2 + 3^2 - 9^2}{2\cdot 3 \cdot 8}\\ &= -\dfrac{1}{6} \end{align*}\]

So \(\boxed{B=99.59^\circ}\). Generally if you can use the law of sines it is easier than the law of cosines. Now that we have one of our angles we can use the law of sines to find another angle, say \(\angle A\).

\[\frac{\sin A}{a} = \frac{\sin B}{b}\]

\[\frac{\sin A}{3} = \frac{\sin 99.59^\circ}{9}\]

\[A =\sin^{-1}\left( \frac{3(\sin 99.59^\circ)}{9} \right)\]

Then \(\boxed{A=19.19^\circ}\) and \(C = 180^\circ -A -B = 180^\circ -19.19^\circ - 99.59^\circ \implies \boxed{C = 61.22^\circ}\).

TipExample 4.2.2

Case 4: Two sides and the included angle (SAS)

Solve the triangle where \(A = 55^\circ\), \(b=3\), and \(c = 10\).

Figure 11

Figure 4.11: Triangle with two sides and included angle

Solution: Figure 4.11 is a sketch of the given information. Once again we can’t use the law of sines because we don’t know an angle and the length of its opposite side. We will start by calculating the length of \(a\) with the law of cosines and then use the law of sines to find another angle. While we could use the law of cosines to do solve for the angle, it is easier to use the law of sines whenever you have the choice. \[\begin{align*} a^2 &= b^2 + c^2 -2bc \cos A\\ &= 3^2 +10^2 -2\cdot 3 \cdot 10 \cos(55^\circ)\\ &= 74.5854 \end{align*}\]

so \(a = 8.64\). Using the law of sines, \(\dfrac{\sin A}{a} = \dfrac{\sin C}{c}\), we can solve for \(C\). (NOTE: Always solve for the largest angle first.)

\[\frac{\sin 55^\circ}{8.64} = \frac{\sin C}{10} \implies C = \sin^{-1}\left( \frac{10 \sin 55^\circ}{8.64} \right) = 108.48^\circ\]

and \(B = 180^\circ - 55^\circ - 108.48^\circ = 16.52^\circ\).

The solution to the triangle is \(\boxed{C= 108.48^\circ, \ B = 16.52^\circ \text{ and } a = 8.64}\).

TipExample 4.2.3

Two radar stations located \(10\) km apart both detect a UFO located between them. Station Alpha calculates the distance to the object to be \(7500\) m and Station Beta calculates the distance as \(9200\) m. Find the angle of elevation measured by both stations (\(\alpha\)) and (\(\beta\)). See Figure 4.12

Figure 12

Figure 4.12: UFO and radar stations

Solution: The triangle formed by the radar stations and the UFO is not a right triangle and we know three sides (SSS). This means we need to use the law of cosines to calculate one of the angles. As before we will use the law of sines to calculate the second angle. Since we are looking for the angle we need the alternate form of the law of cosines: \[\begin{align*} \cos \beta &= \dfrac{a^2 + c^2 - b^2}{2ac}\\ &= \dfrac{9200^2 + 10000^2 - 7500^2}{2(9200)(10000)}\\ &= 0.697772 \end{align*}\]

So \(\beta = \cos^{-1}(0.697772)=45.75^\circ\) and we can use the law of sines to find \(\alpha\). \[\begin{align*} \frac{\sin \alpha}{a} &= \frac{\sin \beta}{b}\\ \frac{\sin \alpha}{9200} &= \frac{\sin 45.75^\circ}{7500}\\ \sin \alpha &= \frac{9200 \sin 45.75^\circ}{7500} \\ \alpha &= 61.48^\circ \end{align*}\]

Then \(\boxed{\alpha = 61.48^\circ \text{ and } \beta = 45.75^\circ}\)

TipExample 4.2.4

A baseball diamond is a square with \(90\) foot sides, with a pitcher’s mound 60.5 feet from home plate. How far is it from the pitcher’s mound to third base? A diagram of the dimensions of a baseball diamond is in Figure 4.13.

Figure 13

Figure 4.13: Dimensions on a baseball diamond

Solution: It is tempting to assume the pitcher’s mound is in the center of the baseball diamond but it is not. It is located about 3 feet closer to home plate than the center. The distance to third base will therefore be different than the distance to home plate. We do have two sides of a triangle and the angle between them. The triangle is drawn on the diagram and the angle is \(45^\circ\) (why?). Using the law of cosines we can find the missing length. \[\begin{align*} a^2 &= b^2 + c^2 - 2bc \cos A \\ a^2 &= 90^2 + 60.5^2 - 2(90)(60.5) \cos 45^\circ \\ a^2 &= 4060 \\ a &= 63.72 \text{ ft} \end{align*}\]

4.2 Exercises

For Exercises 1-6, use the law of cosines to solve the triangle \(\triangle ABC\).

1. 

2. 

3. 

4. 

5. 

6. 

For Exercises 7-12, use the law of cosines to solve the triangle \(\triangle ABC\). If there is more than one possible solution, give both. If there is no answer state that there is no possible triangle.

7. \(a = 10\), \(b=35\), \(c = 30\)

8. \(b = 40\), \(A = 75^\circ\), $c = 35”

9. \(a = 40\), \(B = 25^\circ\), \(c = 30\)

10. \(a = 5\), \(B = 47^\circ\), \(c = 9\)

11. \(a = 12\), \(C = 94^\circ\), \(b = 15\)

12. \(a = 22\), \(b = 40\), \(c = 27\)

For Exercises 13-16, solve for the unknown quantity in Figure 4.14. (Not to scale)

Figure 14: Figure 4.14: UFO and radar stations

13. To find the distance between two radar installations a UFO calculates the distance to installation \(A\) to be \(c = 370\) km, the distance to installation \(C\) to be \(a = 350\) km, and the angle between them \(\beta = 2.1^\circ\). Find the distance between the installations.

14. To find the distance between two radar installations a UFO calculates the distance to installation \(A\) to be \(c = 200\) km, the distance to installation \(C\) to be \(a = 300\) km, and the angle between them \(\beta = 5.0^\circ\). Find the distance between the installations.

15. Two radar stations located 80 km apart both detect a UFO located between them. Station \(A\) calculates the distance to the object to be 20 km and Station \(C\) calculates the distance as 92 km. Find the angles of elevation (\(\alpha\) and \(\gamma\)) measured by both stations.

16. To find the distance between two radar installations a UFO calculates the distance to installation \(A\) to be \(c = 420\) km, the distance to installation \(C\) to be \(a = 150\) km, and the angle between them \(\beta = 4.0^\circ\). Find the distance between the installations.

17. A pilot flies in a straight path for 1 hour 30 min. She then makes a course correction, heading 10 degrees to the right of her original course, and flies 2 hours in the new direction. If she maintains a constant speed of 680 miles per hour, how far is she from her starting position?

18. Two planes leave the same airport at the same time. One flies at 20 degrees east of north at 500 miles per hour. The second flies at 30 east of south at 600 miles per hour. How far apart are the planes after 2 hours?

19. To find the distance across a small lake, a surveyor has taken the measurements shown in Figure 4.15. Find the distance across the lake.

Figure 15

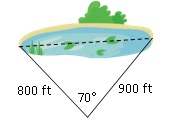
Figure 4.15: Lake width

20. A 127 foot tower is located on a hill that is inclined \(38^\circ\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 64 feet downhill from the base of the tower as seen in Figure 4.16. Find the length of wire needed.

Figure 16

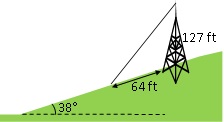
Figure 4.16: Wire length

21. A 113 foot tower is located on a hill that is inclined \(34^\circ\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 98 feet uphill from the base of the tower as seen in Figure 4.17. Find the length of wire needed.

Figure 17

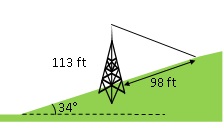
Figure 4.17: Wire length

4.3 Area of a Triangle

Introduction

The formula for the area of a triangle is

\[\text{Area} = \frac{1}{2}(\text{base})\cdot (\text{height}) = \frac{1}{2}b\cdot h\]

Any leg of the triangle can be used as the base but unless you have a right triangle the height is not obvious. The proof of the law of sines provides a way to find the height. Consider either of the triangles in Figure 4.18 where we know the lengths of the sides and the angles.

Figure 18

Figure 4.18: Finding area using height

Now we can calculate the height \(h = c \sin A\) so

\[\text{Area} = \frac{1}{2}b\cdot h = \frac{1}{2}b\cdot c \cdot \sin A\]

This formula works any time you know two sides and the included angle (SAS). The shape of the triangle does not matter.

NoteFormula for the Area of a Triangle

Given a triangle with angles \(A\), \(B\) and \(C\) and sides \(a\), \(b\) and \(c\) opposite those angles

\[\text{Area} = \frac{1}{2}b\cdot h = \frac{1}{2}b\cdot c \cdot \sin A = \frac{1}{2}b\cdot a \cdot \sin C = \frac{1}{2} a\cdot c \cdot \sin B\]

TipExample 4.3.1

Find the area of a triangular lot having two sides of lengths 150 meters and 100 meters with included angle of \(99^\circ\)

Figure 19

Figure 4.19: Triangular lot

Solution: Draw a diagram to represent the problem. Figure 4.19 Then apply the formula \[\begin{align*} \text{Area} &= \frac{1}{2}b\cdot c \cdot \sin A\\ &= \frac{1}{2}\cdot 150\cdot 100 \cdot \sin 99^\circ\\ &= 7407 \text{ m}^2 \end{align*}\]

Heron’s Formula

When you have 3 sides of a triangle and do not know an angle Heron’s formula¹ (sometimes Hero’s formula) can be used. Heron’s formula will not be proved here but can be derived using the law of cosines, the Pythagorean identity and some clever factoring.

NoteHeron’s Formula

Heron’s formula states that the area of a triangle whose sides have lengths \(a\), \(b\) and \(c\) is given by

\[\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}\]

where \(s\) is the semiperimeter

\[s = \frac{1}{2} (a + b + c)\]

TipExample 4.3.2

A surveyor measures the sides of a triangular parcel of land to be 206 feet, 293 feet and 187 feet. Find the area of the parcel.

Solution: When using Heron’s formula find the semiperimeter \(s\) first.

\[s = \frac{1}{2} (a + b + c) = \frac{1}{2} (206+293+187) = 343 \text{ ft}\]

Then calculate the area

\[\begin{align*} \text{Area} &= \sqrt{s(s-a)(s-b)(s-c)}\\ &= \sqrt{343(343-206)(343-293)(343-187)}\\ &= 19100 \text{ ft}^2 \end{align*}\]

TipExample 4.3.3

Find the area of the triangle with side lengths \(a = 1000000\), \(b = 999999.9999979\) and \(c=0.0000029\).

Solution: The problem with this example is that many calculators will not provide the correct answer because of the number of decimal places in the calculation of

\[a + b + c = 2000000.0000008\]

which has 14 digits. While most calculators will store 14 digits internally for calculations they will only display 8 of them. Your calculator may round this to 2000000.0 so when calculating \((s - a)\) you get \((s-a) = (1000000-1000000) = 0\) which gives an area of 0. Clearly this is not the correct answer. The correct answer is

\[\boxed{\text{Area} = 0.99999999999895}\]

There are two alternative forms of Heron’s formula. One from a 13^th century Chinese text by Qin Jiushao

\[\text{Area} = \frac{1}{2}\sqrt{a^2 c^2 - \left( \frac{a^2 + c^2 - b^2}{2}\right)^2} \qquad \text{where} \qquad a \geq b \geq c\]

and one by William Kahan published in 2000. Arrange the sides so that \(a \geq b \geq c\)

\[\text{Area} = \frac{1}{4}\sqrt{[a+(b+c)][c-(a-b)][c+(a-b)][a+(b-c)]}\]

Both of these will provide the correct answer in your calculator if you use all the parentheses and brackets shown.

---

4.3 Exercises

For Exercises 1-6, find the area of the triangle \(\triangle ABC\).

1. 

2. 

3. 

4. 

5. 

6. 

For Exercises 7-12, find the area of the triangle \(\triangle ABC\).

7. \(a = 10\), \(b=35\), \(c = 30\)

8. \(b = 40\), \(A = 75^\circ\), \(c = 35\)

9. \(a = 40\), \(B = 25^\circ\), \(c = 30\)

10. \(a = 5\), \(B = 47^\circ\), \(c = 9\)

11. \(a = 12\), \(C = 94^\circ\), \(b = 15\)

12. \(a = 22\), \(b = 40\), \(c = 27\)

13. Find the area of the quadrilateral in Figure 4.20 below.

Figure 20: Figure 4.20: Quadrilateral for Exercise 13

Footnotes

1. Named after Heron of Alexandria who wrote about it in 60 AD. The formula was discovered independently by the Chinese and their earliest known record of it is from Qin Jiushao in 1247 AD.