8.1 Systems of Linear Equations: Gaussian Elimination
What does it mean to be a solution to a system of equations?
- It is the set of all ordered pairs (\(x\), \(y\)) that satisfy the two equations. You can have one solution, multiple solutions, infinite solutions or no solutions.
Three methods of solution
Graphing:
Graph the two equations and find the intersection.
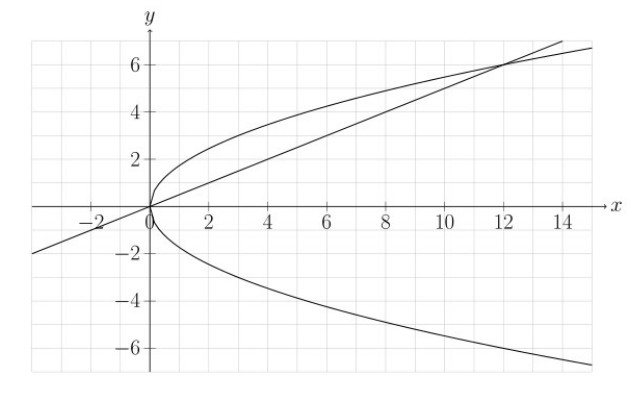
Solve the following system of equations by graphing.
\[\left\{ \begin{array}{rclc}
x - 2y&=&0 & \qquad (1)\\
3x - y^2&=&0 & \qquad (2)\\
\end{array} \right.\]
Substitution
Solve one of the equations for \(x\) or \(y\) and substitute into the other equation.
Use substitution to solve the following system of equations.
\[\left\{ \begin{array}{rclc}
x - 2y&=&0 & \qquad (1)\\
3x - y^2&=&0 & \qquad (2)\\
\end{array} \right.\]
In this case we solve equation (1) for \(x\) and substitute into equation (2).
Elimination
Multiply the equations by appropriate constants so that, when you add the two equations, one variable cancels.
Solve by elimination.
\[\left\{ \begin{array}{rcl}
x + 7y&=&12 \\
3x - 5y&=&10\\
\end{array} \right.\]
Solve by any method.
\[\left\{ \begin{array}{rcl}
6x + 5y&=&-3 \\
-x - \frac{5}{6}y&=&-7\\
\end{array} \right.\]
Solve by any method.
\[\left\{ \begin{array}{rcl}
-\frac{2}{3}x + y&=&-2 \\
2x - 3y&=&6\\
\end{array} \right.\]
Solve by any method.
\[\left\{ \begin{array}{rcl}
2x + 3y&=&18 \\
5x - y&=&11\\
\end{array} \right.\]
Solve by any method.
\[\left\{ \begin{array}{rcl}
\frac{3}{2}x -\frac{1}{5}y&=&8 \\
-2x + 3y&=&3\\
\end{array} \right.\]
Solve by any method.
\[\left\{ \begin{array}{rcl}
y&=&-x \\
y&=&x^3+3x^2+2x\\
\end{array} \right.\]
We saw that we could solve systems of equations using the method of elimination. We can do the same thing for equations with three variables.
\[\left\{ \begin{array}{rcl}
2x + 4y + z&=&1 \\
x - 2y - 3z&=&2\\
x + y - z&=&-1\\
\end{array} \right.\]
If we want to solve these three equations we need a more complicated set of rules. We want to be able to do things which don’t change the value of the system. It turns out that we can do three things.
- Interchange two equations.
- Multiply an equation by a nonzero constant.
- Add a multiple of one equation to another and replace either with the result.
Solve:
\[\left\{ \begin{array}{rcl}
2x-2y +z&=&3 \\
3x+ y- z&=&7\\
x -3y+2z&=&0\\
\end{array} \right.\]
8.6 Partial Fraction Decomposition
Partial Fractions consists of decomposing a rational function into simpler component fractions and then evaluating the integral term by term.
Denominator is a product of distinct linear factors:
\[\frac{3x+7}{x^2+6x+5}\]
Denominator is a product of linear factors, some of which are repeated:
\[\frac{3x^2-8x+13}{(x+3)(x-1)^2}\]
Denominator contains irreducible quadratic factors, none of which is repeated:
\[\frac{2x^2+x-8}{x^3+4x}\]