Chapter 7 Notes, Precalculus 3e Stitz/Zeager
7 Conic Sections
7.2 Circles
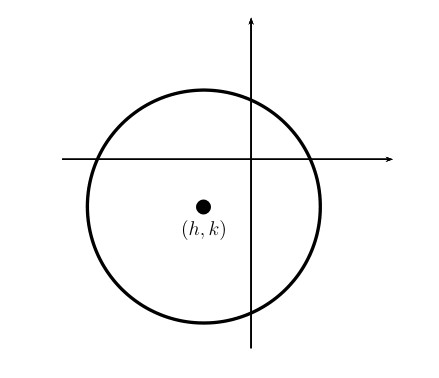
A circle with center \((h, k)\) and radius \(r>0\) is the set of all points \((x,y)\) in the plane whose distance to \((h,k)\) is \(r\).
Standard Equation of a Circle: The standard equation of a circle with center \((h, k)\) and radius \(r>0\) is \[(x-h)^2 + (y-k)^2=r^2\]
7.3 Parabolas
The Parabola
A parabola is the set of all points in a plane equidistant from a fixed point \(F\) (the focus) and a fixed line \(L\) (the directrix) in the plane.
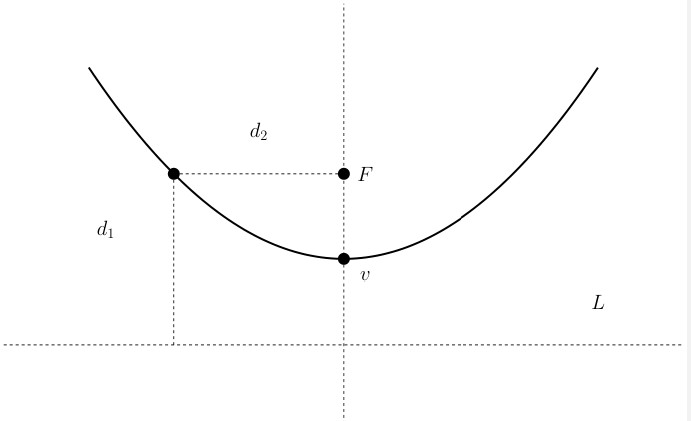
\(d_1=d_2\).
The vertex \(v\) is halfway between the focus and the directrix.
Standard Equations for Parabolas
\((y-k)^2 = 4p(x-h)\) Horizontal axis.
If \(p > 0\) it opens right
If \(p < 0\) it opens left
\((x-h)^2 = 4p(y-k)\) Vertical axis.
If \(p > 0\) it opens up
If \(p < 0\) it opens down
Vertex always located at \((h, k)\).
Focus: \(p\) units from the vertex.
Directrix: \(p\) units from the vertex.
We want the equation to be in form \((y-k)^2 = 4p(x-h)\) so we need to complete the square.
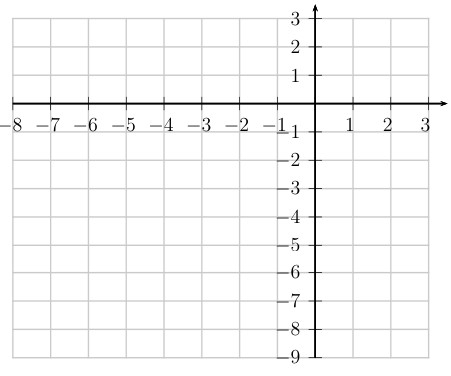
Step 1: Graph the parabola so that we know what it looks like.
Step 1: Clear the denominator.
7.4 Ellipse
An ellipse is the set of all points \(P\) in a plane such that the sum of the distances of \(P\) from two fixed points (\(F\) and \(F'\)) in the plane is constant. \(F\) and \(F'\) are called the foci (plural of focus).
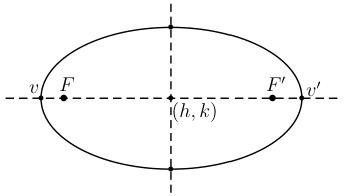
\(d_1 + d_2 =\) constant.
\(F\) and \(F'\) are the foci.
\(v\) and \(v'\) are vertices.
\((h, k)\) is the center.
Label the diagram above with the following:
- major axis
- minor axis
- minor axis vertices: \(B\) and \(B'\)
- distance from foci to center: \(c\)
- distance from vertices to center: \(a\) (major axis) and \(b\) (minor axis)
By using the distance formula we can derive a generic equation for an ellipse.
Standard Equations for Ellipse
Center always located at \((h, k)\).
Major axis length: \(2a\)
Minor axis length: \(2b\)
where \(0 < b < a\)
| Horizontal major axis | Vertical major axis |
|---|---|
| \(\displaystyle \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1\) | \(\displaystyle \frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1\) |
The foci lie on the major axis \(c\) units from the center with \[c^2 = a^2 - b^2\]
Need: \(\displaystyle \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1\) so we complete the square, twice. Once for the \(x\)’s and once for the \(y\)’s.
7.5 Hyperbola
A hyperbola is the set of all points \(P\) in a plane such that the absolute value of the differences of the distances of \(P\) to two fixed points (\(F\) and \(F'\)) in the plane is positive constant. \(F\) and \(F'\) are called the foci (plural of focus).
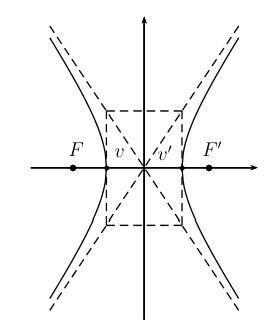
\(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
Center (0, 0)
\(x\)-int: (-\(a\), 0) and (\(a\), 0)
\(y\)-int: NONE
Foci: \(F\) (-\(c\), 0) and \(F'\) (\(c\), 0). \[c^2 = a^2+b^2\]
Transverse axis length = 2\(a\)
Conjugate axis length = 2\(b\)
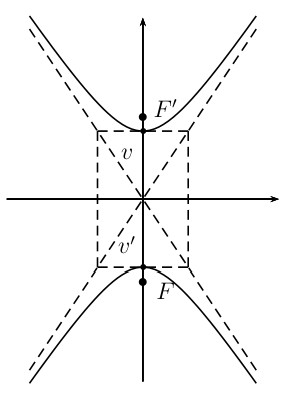
\(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\)
Center (0, 0)
\(x\)-int: NONE
\(y\)-int: (0,-\(a\)) and (0,\(a\))
Foci: \(F\) (0,-\(c\)) and \(F'\) (0,\(c\)). \[c^2 = a^2+b^2\]
Transverse axis length = 2\(a\)
Conjugate axis length = 2\(b\)

Standard Equations for Hyperbola
Center always located at \((h, k)\).
Transverse axis length: \(2a\)
Conjugate axis length: \(2b\)
where \(a > 0\) and \(b > 0\)
| Horizontal transverse axis (\(x\)-intercepts) | Vertical transverse axis (\(y\)-intercepts) |
|---|---|
| \(\displaystyle \frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1\) | \(\displaystyle \frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1\) |
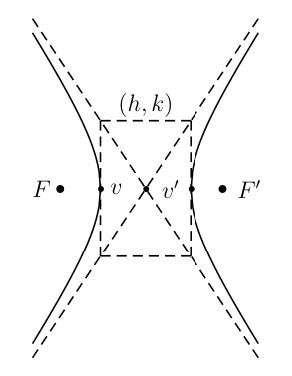
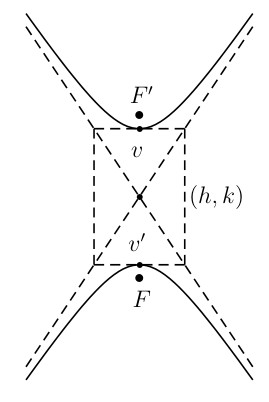
The foci lie on the transverse axis \(c\) units from the center with \[c^2 = a^2 + b^2\]
The asymptote “box” for drawing is determined by:
\(\pm a\) along the transverse axis from the center
\(\pm b\) along the conjugate axis from the center