Chapter 6 Notes, Precalculus 3e Stitz/Zeager

6.1 Introduction to Exponential and Logarithmic Functions

Exponential Functions

The Exponential Function

The exponential function with base $a$ is denoted by \[f(x)=a^x\] where $a \neq 0, ~ a \neq 1$, and $x$ is any real number.

Graphs of exponential functions

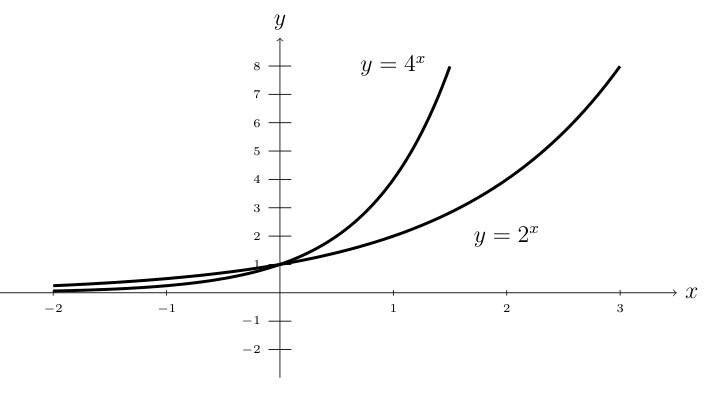
Consider $f(x)=2^x$ and $g(x) = 4^x$.

Let’s look at a table of $x$ and $y$ values for these functions.

$x$	$f(x)$	$g(x)$
-2	1/4	1/16
-1	1/2	1/4
0	1	1
1	2	4
2	4	16
3	8	64

We can graph this data on the $xy$-axes.

Graph showing two exponential functions f(x) equals 2 to the x and g(x) equals 4 to the x, both passing through point (0,1), with f(x) growing more slowly than g(x), demonstrating how larger base values result in steeper exponential growth

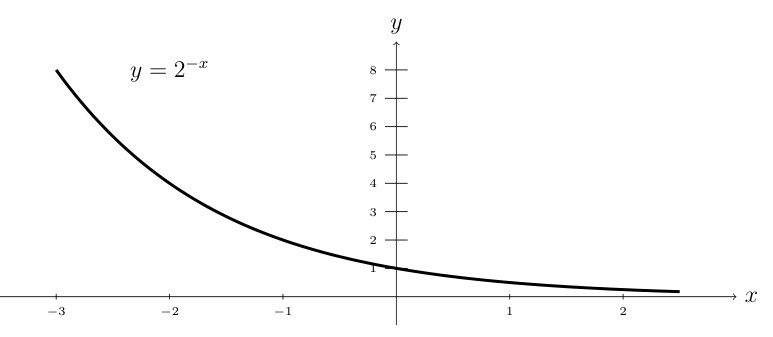
What about the graph of $f(x) = 2^{-x}$?

Graph of exponential decay function f(x) equals 2 to the negative x, showing a decreasing curve passing through (0,1), approaching but never reaching the x-axis as x increases, demonstrating exponential decay behavior

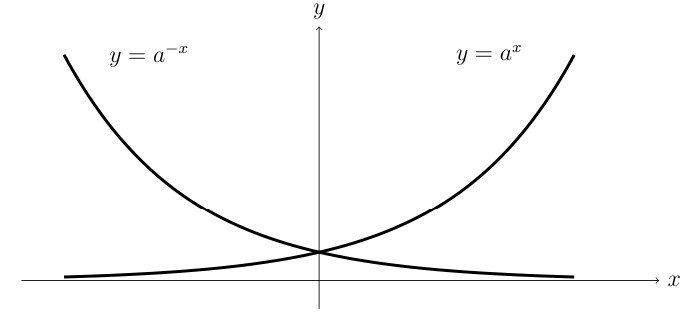
In general we have two basic shapes. $y = a^x$ and $y = a^{-x}$. If we plot them on the same set of axes we can see they are very similar:

Graph comparing exponential growth y equals a to the x and exponential decay y equals a to the negative x on same axes, showing they are reflections of each other across the y-axis, both passing through (0,1), with horizontal asymptote at y equals 0

The Natural Base $e$

The Number $e$

The following limits produce the same number and we call that number $e$. \[\lim_{x \rightarrow \infty} \left(1+\frac{1}{x} \right)^x = e\] \[\lim_{x \rightarrow 0} \left(1+x \right)^{1/x} = e\] $e \approx 2.71828 \ldots$

$e$ is just a number

Since $e$ is a number we can use it in the exponential function $f(x)=e^x$. Why? Because it works in many situations.

Properties of exponents

Let $a$ and $b$ be positive numbers with $a \neq 1$, $b \neq 1$ and let $x$ and $y$ be real numbers. Then:

Exponent Laws:

$a^x a^y = a^{x+y}$
$(a^x)^y = a^{xy}$
$(ab)^x = a^x b^x$
$\displaystyle \left(\frac{a}{b}\right)^x = \frac{a^x}{b^x}$
$\displaystyle \frac{a^x}{a^y} = a^{x-y}$

$a^x = a^y$ if and only if $x=y$.

Logarithms

Let $a > 0$, $a \neq 1$ and $x > 0$ then \[y=\log_a (x) \Longleftrightarrow x=a^y\]

The function $f(x) = \log_a (x)$ is called the logarithmic function with base $a$

OR

“log base $a$”

Example 1

$\log_3 (81) = 4 \Leftrightarrow 3^4 = 81$

$\log_{16} 8 = \frac{3}{4} \Leftrightarrow 16^{3/4} = 8$

$10^{-3} = 0.001 \Leftrightarrow \log_{10}(0.001)=-3$

Example 2

Find $y$. $\qquad$ $\log_5(125)=y$

In words: $\log_a (x)=y$ The logarithm of a number ($x$) is the power ($y$) to which the base ($a$) must be raised to get that number ($x$)

Example 3

Rewrite as an exponential function $\log_2 (1/32) = -5$

Example 4

Rewrite as an exponential function $\log_{16} (2) = 1/4$

Example 5

Rewrite as a logarithmic function $125=5^3$

Graphing logarithms

Suppose we have the function $y = f(x) = b^x$.

Then the inverse function is $x = b^y$ OR $y = f^{-1}(x) = \log_b(x)$. So the logarithm is the inverse of the exponential function.

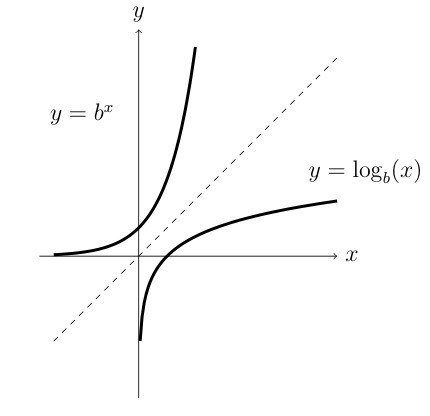
Graph showing exponential function y equals b to the x and its inverse logarithmic function y equals log base b of x reflected across the line y equals x, demonstrating the inverse relationship between exponential and logarithmic functions

Since the two functions are inverses of each other then \[b^{\log_b(x)}=x \qquad \text{AND} \qquad \log_b(b^x) = x\]

Example 6

Simplify $\log_2(64)$

Properties of Logarithms

Let $b$ be a positive real number with $b \neq 1$, and let $x$ be any real number. Then:

$\log_b(1) = 0$ $\qquad$ i.e. $b^0 = 1$
$\log_b(b) = 1$ $\qquad$ i.e. $b^1 = b$
$\log_b(b^x) = x$ $\qquad$ i.e. $b^x = b^x$
$b^{\log_b(x)} = x$ if $x>0$

The natural logarithm

This is the same as before but now we use base $e$ where $e$ is the number we found in the previous section. Since the log base $e$ shows up so often we call it the natural log. \[\log_e(x) = \ln(x)\]

We also use log base 10 very often so we abbreviate that as \[\log_{10}(x) = \log(x)\]

Your calculator follows the same convention.

Example 7

Evaluate the following logarithms without a calculator:

$\log(1000)$

$\log_9(243)$

$\log_b(b^{-3})$

$\ln(e^{-2})$

Example 8

Evaluate with your calculator:

$\log(345)$

$\log(4/5)$

$3 \ln(1+\sqrt{3})$

Example 9

6.2 Properties of Logarithms

Change of Base Formula

Let $a, b, x$ be positive real numbers with $a \neq 1, b\neq 1$. Then \[\log_a(x)=\frac{\log_b(x)}{\log_b(a)} \qquad \text{(For any $b$)}\]

For the calculator you can use either base 10 or base $e$. \[\log_a(x)=\frac{\log(x)}{\log(a)} \qquad \text{OR} \qquad \log_a(x)=\frac{\ln(x)}{\ln(a)}\]

Example 10

Evaluate on a calculator using both common and natural logs. $\log_7(4)$

Example 11

Convert $60(1.08)^t = 3360$ to logarithmic form and solve for $t$

Important Properties of Logarithms

Let $b$, $M$, $N$ be positive real numbers with $b \neq 1$, and let $p$ be any real number. Then:

$\log_b(MN) = \log_b(M) + \log_b(N)$
$\log_b\left(\frac{M}{N}\right) = \log_b(M) - \log_b(N)$
$\log_b(M^p) = p\log_b(M)$
$\log_b(M) = \log_b(N) \Longleftrightarrow M = N$

Example 12

Use the properties of logs to rewrite the following expressions.

$\log_{10}(10z) =$

$\log_6\left(\frac{y}{2}\right) =$

$\log_5(\sqrt[3]{5}) = \log_5\left(5^{1/3}\right) =$

$\displaystyle \ln\left(\frac{x^2-1}{x^3}\right)$

$\displaystyle \log\left(\frac{\sqrt{x} y^4}{z^4}\right)$

Example 13

Use the properties of logs to rewrite the following expressions as a single logarithm.

$\ln(x-2) - \ln(x+2) =$

$\log_b w + \log_b x - \log_b y =$

$4[\ln z + \ln(z + 5)] - 2\ln(z-5) =$

Example 14

Solve without a calculator: $\log_4 2 + \log_4 32 =$

Example 15

More examples:

Simplify by using common logarithms: $\log_2(29)$

Simplify by using natural logarithms: $\log_4 7$

Write the expression in terms of $\ln 5$ and $\ln 3$: $\displaystyle \ln\frac{5}{81}$

Expand the logarithmic expression: $\displaystyle \ln\frac{\sqrt[7]{x-1}}{2}$

Use the properties of logarithms to expand the expression: $\log_6 (12xy^3)$

Write as a single logarithm: $\displaystyle \frac{1}{3}[\log_6 x + \log_6 (x+7)]$

Write as a single logarithm: $\displaystyle \frac{1}{8}[\log_8 (x-4) + 5 \log_8 (x^2+9)]$

6.3 Exponential Equations

Recall: \[a^x=a^y ~ \Longleftrightarrow ~ x = y\] and \[\log_ax = \log_a y~ \Longleftrightarrow ~ x = y\]

Example 16

Solve for $x$ in the following equations:

$64^{x+3}=16$

$3^x = 243$

$\displaystyle \left(\frac{1}{4}\right)^x=64$

$2^{x-3} = 32$

$e^{9x} = 15$

$2+e^{x+2} = 32$

Example 17

Solve for $x$:

$e^{2x} = 50$

$6^{5x}=3000$

$\displaystyle \frac{119}{e^{6x} - 14} = 7$

6.4 Logarithmic Equations

Example 18

Which of the following are equivalent to $3 \cdot \log\left(u^{-1/7}\right)$:

$\log\left( \dfrac{1}{\sqrt[7]{u^3}} \right)$
$-\dfrac{3}{7} \log\left( u \right)$
$\log\left( \dfrac{1}{u^{3/7}} \right)$
$-\dfrac{1}{7}\log\left( u^3 \right)$
$-\log\left( u^{3/7} \right)$

Example 19

Solve for $x$ in the following equations:

$\ln x - \ln 5 = 0$

$\log_x 625 = 4$

$\ln (2x-1) = 0$

$5+5\ln x = 30$

$\log 2x - \log 8x^2 = 3$

Example 20

Simplify the following:

$\log_6 6^{2x-1}$

$\ln e^{x^4}$

Example 21

Solve for $x$:

$\ln 4x = 1$

$\log_6 6x + \log_6(x+5) = 2$

$\log_6 x^2 - \log_6 (x+1) = 2$

6.5 Exponential and Logarithmic Models

Finance: Compound interest.

$P$ is some principal amount of money.

$r$ is the interest rate per year.

Simple interest:

After 1 year we have $P_1 = P +rP = P(1+r)$

After 2 year we have $P_2 = P_1 +rP_1 = P_1(1+r)=P(1+r)(1+r)=P(1+r)^2$

In fact at year $t$ you have \[P_t = P(1+r)^t\]

If you compound each month then you have to add 1/12 of the interest every month and you get \[P_t = P\left(1+\frac{r}{12}\right)^{12t}, \qquad \text{where } t = \text{number of years}\]

In general if you compound $n$ times per year you have \[P_t = P\left(1+\frac{r}{n}\right)^{nt}\]

If we compound continuously that mean $n \rightarrow \infty$ so \[P_t = Pe^{rt}\]

Example 22

My credit card has $4000 on it. The interest rate is 18% per year. If I make no payments how much do I owe at the end of three years if the credit card company compounds the interest (a) yearly, (b) monthly, (c) daily, and (d) continuously?

Example 23

We would like to have $50000 in our investment account at the end of $t$ years. Find the amount of principal $P$ that must be invested at 9.5% compounded continuously if:

$t=1$ year

$t = 10$ years

$t = 50$ years

Example 24

Find the time required to double an investment of $P_0$ dollars if the interest rate is 6% compounded continuously.

The formula for interest compounded continuously is \[P_t = P_0 e^{rt}\]

To double the investment we want to find the value of $t$ when $P_t = 2P_0$.

Example 25

The population of a city is \[P=240360 e^{0.012 t}\] where $t=0$ represents the year 2000. According to this model when will the population reach 275000?

Example 26

The number of bacteria $N$ in a culture is modeled by \[N=250e^{kt}\] where $t$ is the time in hours. After 10 days the population is 280 bacteria. (i.e. $N = 280$ when $t = 10$), estimate the time required to double the population.

step 1: Find $k$ by solving the formula $280 = 250 e^{k(10)}$.

step 2: Find $t$ for $N = 2(250) = 500$. (double the original population)

Example 27

Carbon 14 ($^{14}$C) has a half life of 5730 years. (Half life is the amount of time for half the original material to decay.) Carbon 14 dating assumes that the carbon dioxide today has the same amount of radioactive material as it did centuries ago. If this is true, the amount of $^{14}$C absorbed by a tree centuries ago should be the same as a tree growing today. A piece of ancient coal has 15% as much $^{14}$C as a piece of modern coal. How long ago was the tree burned to make the ancient coal?

Decay Model: \[A = A_0 e^{-kt}\] where $A_0$ is the original amount of material, $k$ is the decay constant and $A$ is the amount of material left after $t$ years.

Step 1: Find $k$ using the half life. $\frac{1}{2} A_0 = A_0 e^{-k 5730}$

Step 2: Find $t$ for $0.15 A_0 = A_0 e^{-kt}$.

6 Exponential and Logarithmic Functions

6.1 Introduction to Exponential and Logarithmic Functions

Exponential Functions

Logarithms

Graphing logarithms

The natural logarithm

6.2 Properties of Logarithms

6.3 Exponential Equations

6.4 Logarithmic Equations

6.5 Exponential and Logarithmic Models