Chapter 5: Further Topics in Functions, Precalculus 3e Stitz/Zeager

Author

Chalmeta

5.1 Function Composition

Composition of Function

The composition of a function \(f\) with a function \(g\) is:

\[(f \circ g)(x) = f(g(x))\]

The domain of \((f \circ g)\) is the set of all \(x\) in the domain of \(g\) such that \(g(x)\) is in the domain of \(f\).

TipExample 5.1.1

Suppose \(f(x) = x^3 + 2x +1\) and \(g(x) = x - 1\) then find:

  1. \((f \circ g)(x) = f(g(x)) = f(x - 1)\)
  1. \((g \circ f)(x) = g(f(x)) = g(x^3 +2x +1)\)
  1. \((f \circ f)(x) = f(f(x)) = f(x^3 +2x +1)\)
TipExample 5.1.2

Find (a) \((f \circ g)(x)\), (b) \((g \circ f)(x)\) and (c) the domain of each for \(f(x) = \sqrt{x-4}\) and \(g(x) = x^2\).

TipExample 5.1.3

Find (a) \((f \circ g)(x)\), (b) \((g \circ f)(x)\) and (c) the domain of each for \(f(x) = \dfrac{1}{x-4}\) and \(g(x) = \dfrac{2}{x}+2\).

TipExample 5.1.4

Find functions \(f\) and \(g\) such that \(h(x) = \sqrt[3]{x^2-4} = (f \circ g)(x)\).

TipExample 5.1.5

Let \(f(x) = \sqrt{90-x}\) and \(g(x) = x^2 - x\). Find \((f \circ g)(x)\) and its domain.

TipExample 5.1.6

Use the functions below to find the compositions.

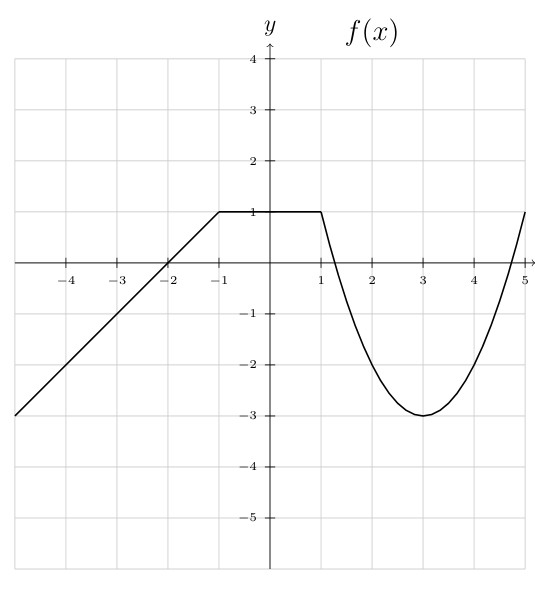
Graph of function f(x) on a coordinate plane with gridlines. The x-axis ranges from -4 to 5 and the y-axis from -5 to 4. The function consists of three pieces: a linear segment from lower left rising to approximately (-1, 1), a horizontal segment at y = 1 from x = -1 to x = 1, and a parabola opening downward from x = 1 to x = 5 with minimum around y = -3 near x = 3. The graph is labeled f(x).

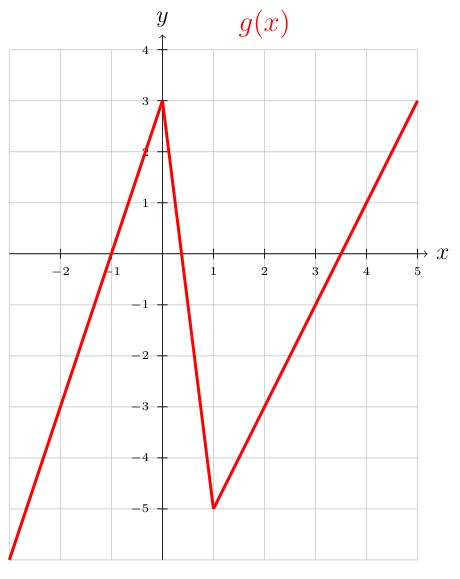
Graph of function g(x) in red on a coordinate plane with gridlines. The x-axis ranges from -2 to 5 and the y-axis from -5 to 4. The function shows a V-shaped graph with a sharp peak at approximately (0, 3), descending steeply to a valley around (1, -5), then rising linearly toward the upper right. The graph is labeled g(x) in red.

  1. \(f(g(1))\)
  1. \(g(f(2))\)
  1. \(f(g(0))\)
  1. \(g(f(0))\)
  1. \(f(g(-2))\)
  1. \(g(f(-2))\)

5.2 Inverse Functions

One to one functions

A function is said to be one to one (1-1) if no two ordered pairs have the same second component but different first component.

A function has one \(y\) value for each \(x\) value but those \(y\) values can repeat. In a 1-1 function the \(y\) values never repeat.

Graphically:

An equation must pass the Vertical Line Test to be a function.

A function must pass the Horizontal Line Test to be 1-1.

TipExample 5.2.1

\(f(x)=x^2\) is not 1-1. \(\qquad\) \(f(x) = x^3\) is 1-1.

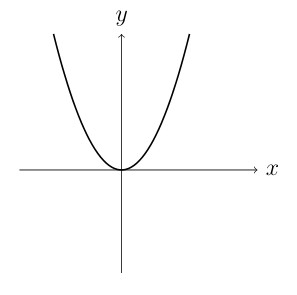
Graph of parabola f(x) = x² opening upward with vertex at the origin. The curve is symmetric about the y-axis. A horizontal line drawn across the parabola would intersect it at two points, demonstrating that the function fails the horizontal line test and is therefore NOT one-to-one.

NOT 1-1 (fails horizontal line test)

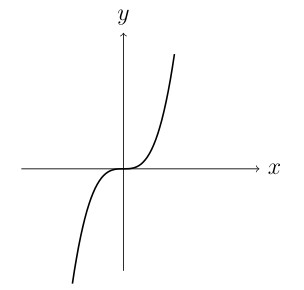
Graph of cubic function f(x) = x³ showing the characteristic S-shaped curve passing through the origin. The curve extends from lower left to upper right. Any horizontal line drawn would intersect the curve at exactly one point, demonstrating that the function passes the horizontal line test and IS one-to-one.

IS 1-1 (passes horizontal line test)

Inverses

The identity function is \(f(x) = x\) or \(y = x\). You get out what you put in. Given a function \(f\) that is 1-1 then \(f\) has an inverse \(f^{-1}\) and:

\[f(f^{-1}(x)) = x \qquad \text{and} \qquad f^{-1}(f(x)) = x\]

If \(f\) is not 1-1 then \(f^{-1}\) DOES NOT EXIST.

Graphically

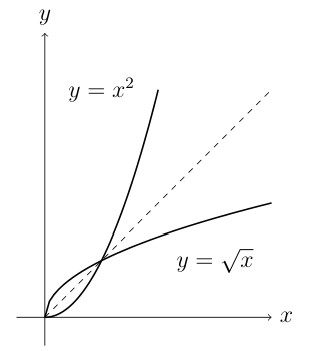
Graph showing a function and its inverse reflected across the line y = x (shown as a dashed line). The original cubic-like function curves from lower left to upper right. Its inverse function is the reflection across the diagonal line y = x, demonstrating the geometric relationship between a function and its inverse: if point (a,b) is on f(x), then point (b,a) is on f⁻¹(x).

TipExample 5.2.2

Draw the inverse of the following function on the same set of axes.

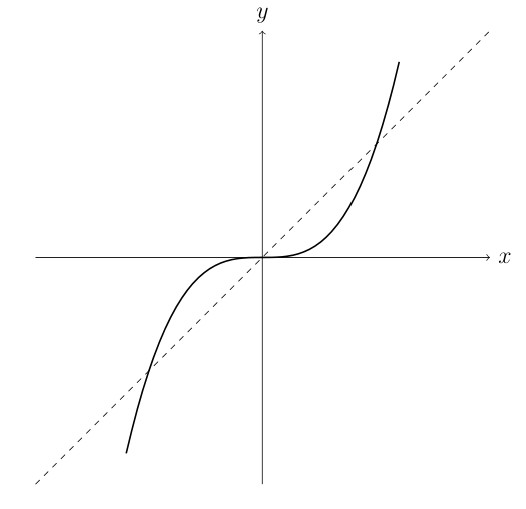
Graph of a cubic function showing an S-shaped curve with a dashed diagonal line y = x. The cubic function passes through the origin and extends from lower left to upper right. Students are to draw the inverse function by reflecting the given curve across the line y = x.

Finding inverses from tables and graphs

TipExample 5.2.3

Use the table below to fill in the missing values.

\(x\) 0 1 2 3 4 5 6 7 8 9
\(f(x)\) 8 4 5 7 2 1 6 9 3 0

  1. \(f(2) =\)

  2. if \(f(x)=4\) then \(x =\)

  3. \(f^{-1}(5) =\)

  4. if \(f^{-1}(x) =1\) then \(x =\)

TipExample 5.2.4

Use the graph below to fill in the missing values.

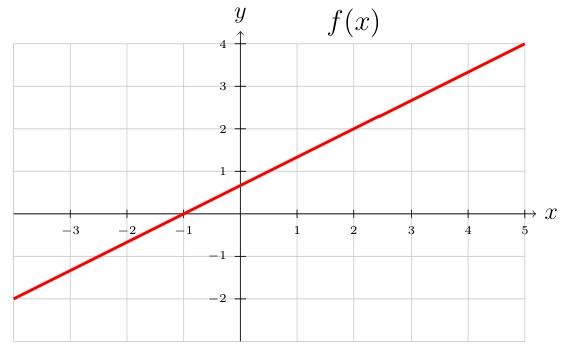
Graph of a linear function f(x) shown in red on a coordinate plane with gridlines. The line has positive slope and passes through the origin, extending from lower left to upper right across the visible domain from approximately x = -3 to x = 5, with y-values ranging from approximately -2 to 4.

  1. \(f(2) =\)

  2. if \(f(x)=4\) then \(x =\)

  3. \(f^{-1}(-2) =\)

  4. \(f^{-1}(0) =\)

  5. if \(f^{-1}(x) =5\) then \(x =\)

Finding Inverses Algebraically

Step 1: Solve for \(x\).

Step 2: Check the domain.

Step 3: Switch \(x\) and \(y\).

Step 4: Write \(f^{-1}(x) =\)

Step 5: Check that \(f(f^{-1}(x)) = x\).

TipExample 5.2.5

Let \(f(x) = (x+4)^2\).

  1. Find the domain on which \(f\) is one-to-one and non-decreasing.
  1. Find the inverse of \(f\) restricted to this domain.

Step 1: Solve for \(x\). (two answers here)

Step 2: Check the domain.

Step 3: Switch \(x\) and \(y\).

Step 4: Write \(f^{-1}(x) =\)

Step 5: Check that \(f(f^{-1}(x)) = x\).

TipExample 5.2.6

Find the inverse of \(f(x) = \frac{2x-5}{-4x-2}\).