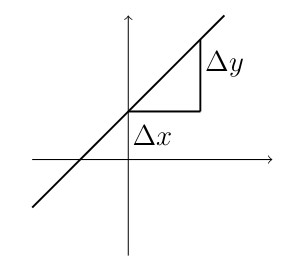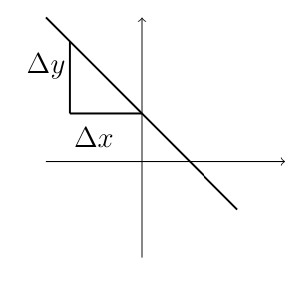2.1 Linear Equations in Two Variables
Parallel and Perpendicular Lines
Parallel lines have the same slope. If \(y = m_1 x + b_1\) is parallel to \(y = m_2 x + b_2\) then \(m_1 = m_2\).
Perpendicular lines have negative reciprocal slopes. If \(y = m_1 x + b_1\) is perpendicular to \(y = m_2 x + b_2\) then \(m_1 = -\frac{1}{m_2}\) and \(m_2 = -\frac{1}{m_1}\).
Write the equations of the lines parallel and perpendicular to \(-4x + 2y = 3\) passing through the point (2, 1).
2.2 Absolute Value Functions
Definition: The absolute value of a real number \(x\), denoted \(|x|\), is given by:
\[|x| = \begin{cases}
-x, & \text{if } x < 0 \\
x, & \text{if } x \geq 0
\end{cases}\]
Absolute Value Properties
- Product rule: \(|ab| = |a| |b|\)
- Power rule: \(|a^n| = |a|^n\)
- Quotient rule: \(\left|\frac{a}{b}\right| = \frac{|a|}{|b|}\)
- Equality property 1: \(|x|=0\) if and only if \(x=0\)
- Equality property 2: For \(c>0\), \(|x|=c\) if and only if \(x=c\) or \(x = -c\).
- Equality property 3: For \(c<0\), \(|x|=c\) has no solution.
An equation with an absolute value is always TWO equations:
\[|x-5| = 4 \qquad \implies \qquad x-5=4 \text{ OR } -(x-5) = 4\]
We start by getting the absolute value by itself on one side of the equation.
ALWAYS check your solutions:
Sketch a graph of \(f(x) = \frac{1}{2} |x-1|-3\)
2.3 Quadratic Functions
Definition: Let \(a\), \(b\), and \(c\) be real numbers with \(a \neq 0\). The function:
\[f(x) = ax^2 + bx + c\]
is called a quadratic equation.
The graph of a quadratic equation is a parabola. All parabolas are symmetric with respect to the axis of symmetry which passes through the vertex.
\[f(x)=x^2+2x+1 \qquad \text{OR} \qquad f(x) = -x^2-2x-1\]
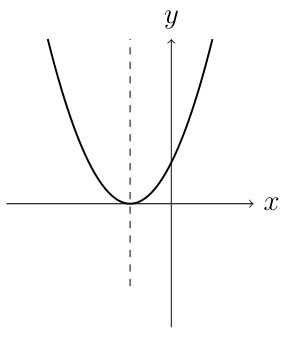
\(a>0\) graph opens up
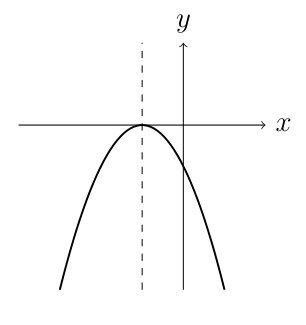
\(a<0\) graph opens down
The Standard Form of a Parabola
\[f(x)=a(x-h)^2+k\]
Vertex is located at \((h, k)\)
if \(a>0\) graph opens up
if \(a<0\) graph opens down
Alternate form
If \(f(x)= ax^2+bx+c\) then the:
\[\text{vertex} = \left(\frac{-b}{2a}, ~ f\left(\frac{-b}{2a}\right)\right)\]
To Graph a Parabola
- Find the vertex
- Find the \(x\)-intercepts
- Determine if it opens up or down
- Sketch
Graph \(f(x) = 2x^2-12x-14\).
Step 1: Vertex:
\(x = \frac{-(-12)}{2(2)} = 3\)
\(y = f(3) = 2(9)-12(3)-14 = -32\)
So the coordinates of the vertex are \((x, y) = (3, -32)\)
Step 2: \(x\)-intercepts:
\[0 = 2x^2-12x-14\]
Step 4: Sketch
Step 4: Sketch
Find the standard form for a parabola that has (0, 1) as its vertex and passes through the point (1, 0)
Convert to standard form \(f(x) = x^2+6x +5\) and graph.
Convert to standard form \(f(x) = x^2-2x -8\) and graph.
- \(9x\cdot (x-3)+7\cdot (x-3)\)
- \(x^3 - 8x^2+15x\)
- \(x^2+11x+28\)
- \(6t^2+5t -4\)
- \(5z^2+23z+12\)
A rancher has 260 yards of fence with which to enclose three sides of a rectangular meadow (the fourth side is a river and will not require fencing). Find the dimensions of the meadow with the largest possible area.
A person standing close to the edge on top of a 72-foot building throws a ball vertically upward. The quadratic function \(h(t) = -16t^2 +84t+72\) models the ball’s height about the ground, \(h(t)\), in feet, \(t\) seconds after it was thrown.
What is the maximum height of the ball?
How many seconds does it take until the ball hits the ground?
2.4 Solving Inequalities with Absolute Value and Quadratic Functions
Interval Notation
| \(x > 2\) |
|
\((2, \infty)\) |
| \(x \geq 2\) |
|
\([2, \infty)\) |
| \(x \geq 2\) AND \(x \leq 4\) |
\(2 \leq x \leq 4\) |
\([2, 4]\) |
| \(x \leq 2\) OR \(x \geq 4\) |
|
\((-\infty, 2] \cup [4, \infty)\) |
Properties of Inequalities
- Transitive: \(a < b\) and \(b < c \implies a < c\)
- Addition of Constants: If \(a < b\) then \(a+ c < b + c\)
- Addition: If \(a < b\) and \(c < d\) then \(a +c < b + d\)
- Multiplication by a constant:
- If \(c > 0\) and \(a < b\) then \(ac < bc\)
- If \(c < 0\) and \(a < b\) then \(ac > bc\)
NOTE: If you multiply or divide by a negative number you reverse the order of the inequality.
Solving linear inequalities
\(10x < 40\)
\(-10x < 40\)
\(4(x+1) \leq 2x+3\)
\(-8 \leq -(3x+5) < 13\)
Absolute value and inequalities
Absolute value is still two equations
\(\left|\frac{x}{2}\right| > 5\)
\[\frac{x}{2} > 5 \qquad \text{OR} \qquad -\frac{x}{2} > 5\]
\(|x-7| < 5\)
\[-5 < x-7 < 5\]
Question: What does \(|x-2| < 5\) mean?
Answer: All real numbers within five units of two.
So all real numbers within 5 units of 8 would be written as:
And all real numbers at least 5 units from 8 would be written as:
Solving polynomial inequalities
Step 1: Set equation equal to zero and find the zeros. (Factor)
Step 2: Set up a table of signs
Step 3: Find where the table gives negative values and write the solution
\((x-1)^2(x+2)^3 \geq 0\)