Chapter 1 Notes, Precalculus 3e Stitz/Zeager

Author

Chalmeta

1.1 Sets of Real Numbers and the Cartesian Coordinate Plane

Sets and Interval Notation

Definition: Suppose $A$ and $B$ are two sets.

The intersection of $A$ and $B$: $A \cap B = \{ x \, | \, x \in A \, \text{and} \,\, x \in B \}$
The union of $A$ and $B$: $A \cup B = \{ x \, | \, x \in A \, \text{or} \,\, x \in B \, \, \text{(or both)} \}$

Interval and Inequality Notation, Numberlines

Expression	Number Line
$x > 2$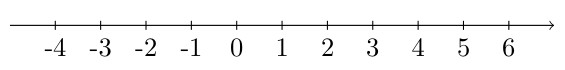
$x \geq 2$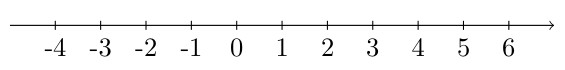
$x \geq 2$ AND $x \leq 4$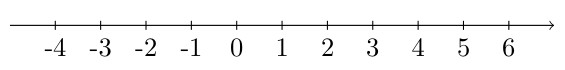


$x \leq 2$ OR $x \geq 4$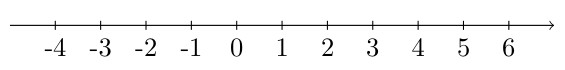


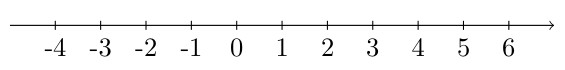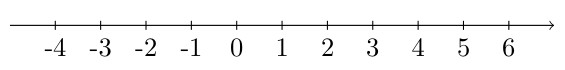$x \leq 2$ AND $x \geq 4$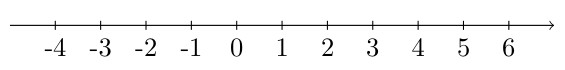

Interval Notation

Inequality notation	Inequality notation	Interval notation
$x > 2$		$(2, \infty)$
$x \geq 2$		$[2, \infty)$
$x \geq 2$ AND $x \leq 4$	$2 \leq x \leq 4$	$[2, 4]$
$x \leq 2$ OR $x \geq 4$		$(-\infty, 2] \cup [4, \infty)$

Cartesian Coordinates and Symmetry

All points in the plane are ordered pairs $(x, y)$ where the 1st coordinate is directed distance on the $x$-axis and the 2nd coordinate is directed distance on the $y$-axis. The $xy$-plane is divided into four quadrants labeled I, II, III, and IV.

Cartesian coordinate plane showing the x and y axes from -4 to 4 on both axes, with grid lines and four quadrants labeled. Quadrant I is in the upper right (positive x, positive y), Quadrant II in the upper left (negative x, positive y), Quadrant III in the lower left (negative x, negative y), and Quadrant IV in the lower right (positive x, negative y). The origin (0,0) is at the intersection of the axes.

Example 1.1.1

At various times, the amount of water in a tub was measured and recorded in the table of values. Sketch a plot of the data.

Time (min)	Water in tub (gallons)
0	0
1	8
3	24
4	32

The Distance Formula

Diagram showing two points P₁(x₁,y₁) and P₂(x₂,y₂) connected by a line segment, illustrating the distance formula with a right triangle formed by horizontal and vertical components.

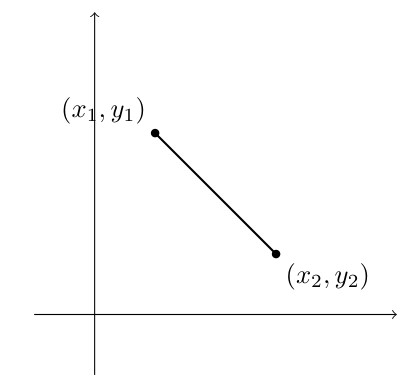
The distance between two points is given by:

\[d = \sqrt{(x_2-x_1)^2+(y_2 - y_1)^2}\]

The Midpoint Formula

Diagram showing two points P₁(x₁,y₁) and P₂(x₂,y₂) with the midpoint M marked at the center of the line segment connecting them.

The midpoint between two points is given by:

\[\text{M.P.} = \left(\frac{x_2 + x_1}{2}, \frac{y_2 + y_1}{2}\right)\]

Example 1.1.2

Find the distance and midpoint between $P(3, -10)$ and $Q(-1, 2)$

Example 1.1.3

The midpoint of $AB$ is at $(1,-5)$. If $A=(-3,7)$, find $B$.

Definition: Two points $(a,b)$ and $(c,d)$ in the plane are said to be

symmetric about the $x$-axis if $a = c$ and $b = -d$
symmetric about the $y$-axis if $a = -c$ and $b = d$
symmetric about the origin if $a = -c$ and $b = -d$

Shifting Points (Reflections)

To reflect a point $(x,y)$ about the:

$x$-axis, replace $y$ with $-y$.
$y$-axis, replace $x$ with $-x$.
origin, replace $x$ with $-x$ and $y$ with $-y$.

Example 1.1.4

Use the graph below to:

Reflect the triangle over the $x$-axis.
Reflect triangle over the $y$-axis.
Reflect triangle over the origin.

Coordinate plane with grid ranging from -6 to 6 on the x-axis and -7 to 7 on the y-axis. A triangle is drawn in the upper left quadrant with vertices approximately at (-6, 3), (-4, 6), and (-3, 2). The triangle has solid lines forming its three sides. This is the original triangle that students will reflect across the x-axis, y-axis, and origin to practice symmetry transformations.

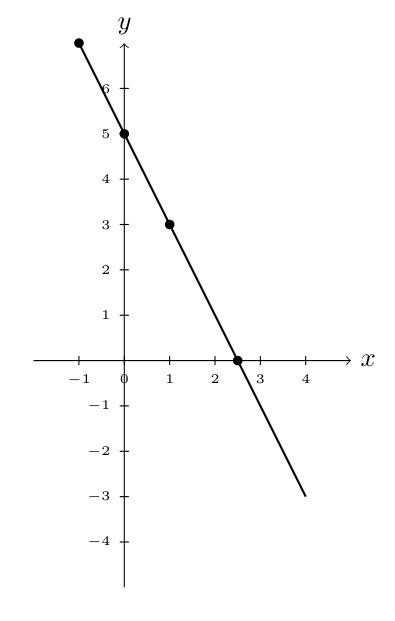
1.2 Relations

We reviewed in Section 1.1 how to graph points so now we want to know how to graph equations. Suppose we want to graph the equation $y=-2x+5$. This is a relationship between $x$ and $y$ where the value of $y$ is determined by the choice of $x$. For each $x$ we can find a $y$ value and that is one point $(x, y)$ on the graph:

$x$	$y=-2x+5$
-1	$(-2)(-1)+5 = 7$
0	$(-2)(0)+5 = 5$
1	$(-2)(1)+5 = 3$
2	$(-2)(2)+5 = 1$
5/2	$(-2)(5/2)+5 = 0$

Graph of the line y = -2x + 5 plotted on a coordinate plane. The line has negative slope (-2) and y-intercept at (0,5). It passes through points including (-1,7), (0,5), (1,3), (2,1), and (5/2,0), showing a downward slant from left to right. The line extends across the visible coordinate plane demonstrating the linear relationship between x and y.

$x$ and $y$ Intercepts

Intercept	Description	How to Find
$x$-intercept	The point where the graph crosses the $x$-axis	Set $y = 0$
$y$-intercept	The point where the graph crosses the $y$-axis	Set $x = 0$

Example 1.2.1

Find all intercepts for $y=4x^3-16x$.

Symmetry

Symmetric about $y$-axis

A graph is symmetric about the $y$-axis if it is the same on both sides of the $y$-axis.

Thus when $(a, b)$ is on the graph then $(-a, b)$ is also on the graph.

$f(x) = f(-x)$ for all $x$.

Graph showing y-axis symmetry with a parabola y = x². The parabola opens upward with vertex at the origin, demonstrating that the graph is a mirror image across the y-axis. Points (a,b) and (-a,b) are symmetrically positioned on either side of the y-axis, illustrating that f(x) = f(-x).

Symmetric about $x$-axis

A graph is symmetric about the $x$-axis if it is the same on both sides of the $x$-axis.

Thus when $(a, b)$ is on the graph then $(a, -b)$ is also on the graph.

Graph showing x-axis symmetry with a sideways parabola x = y². The parabola opens to the right with vertex at the origin, demonstrating that the graph is a mirror image across the x-axis. Points (a,b) and (a,-b) are symmetrically positioned above and below the x-axis.

Symmetric about the origin

A graph is symmetric about the origin if the graph is unchanged by a 180 degree rotation about the origin.

Thus when $(a, b)$ is on the graph then $(-a, -b)$ is also on the graph.

Graph showing origin symmetry with a cubic function y = x³. The curve passes through the origin and demonstrates rotational symmetry: when rotated 180 degrees about the origin, the graph looks identical. Points (a,b) and (-a,-b) are symmetrically positioned, illustrating that if (a,b) is on the graph, then so is (-a,-b).

The short version

Symmetry	The equation is equivalent when…
$y$-axis	$x$ is replaced with $-x$
$x$-axis	$y$ is replaced with $-y$
origin	$x$ and $y$ are replaced by $-x$ and $-y$

Example 1.2.2

Find the symmetry of $y = x^3$.

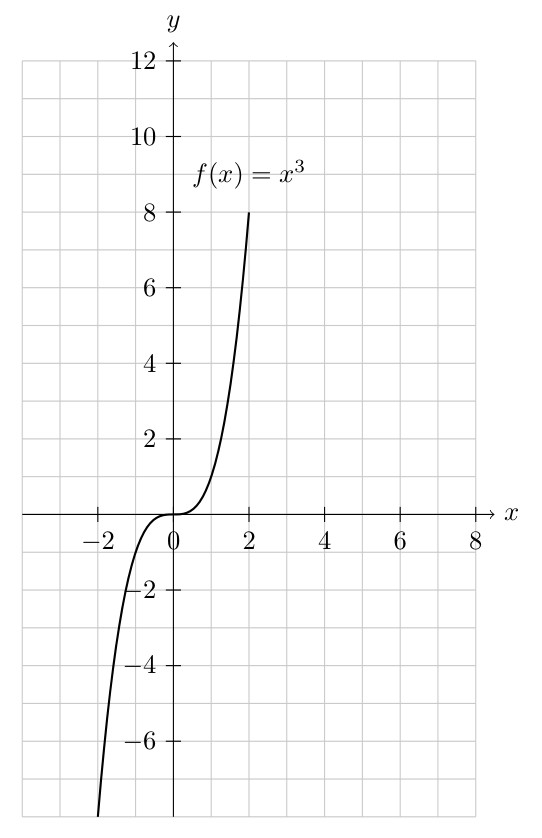
Try replacing $x$ with $-x$:

\[\begin{align*} y &= x^3\\ y &= (-x)^3 \end{align*}\]

Try replacing $y$ with $-y$:

\[\begin{align*} y &= x^3\\ -y &= (x)^3 \end{align*}\]

Try replacing $x$ with $-x$ and $y$ with $-y$:

\[\begin{align*} y &= x^3\\ -y &= (-x)^3 \end{align*}\]

Draw a sketch: Since we have origin symmetry we can just plot a few positive numbers.

Example 1.2.3

Find the intercepts, determine if there is any symmetry and graph the function:

\[x^2+y^3=1\]

Example 1.2.4

Find the intercepts, determine if there is any symmetry and graph the function:

\[x=2y^3+3y\]

Example 1.2.5

Sketch the graph of $3x+2y=-6$

1.3 Introduction to Functions

Definition: A function is a rule that establishes a correspondence between two sets of elements (called the domain and range) so that for every element in the domain there corresponds EXACTLY ONE element in the range.

Definition: A function in one variable is a set of ordered pairs with the property that no two ordered pairs have the same first element.

For example: $\{(-2, 1), (-1, 2), (0, 3), (1, 4), (2, 5)\}$.

Definition:

Domain: The “things” you can put into a function.

Range: The “things” you get out of a function.

Graphically

An equation defines a function if each vertical line drawn passes through the graph at most once. This is called the Vertical Line Test.

For example:

Graph of a circle centered at the origin. When a vertical line is drawn through the circle, it intersects the curve at two points (except at the leftmost and rightmost points), demonstrating that a circle fails the vertical line test and is NOT a function. The circle shows that for most x-values, there are two corresponding y-values.

NOT a function (fails vertical line test)

Graph of a cubic function f(x) = x³, showing the characteristic S-shaped curve passing through the origin. When any vertical line is drawn, it intersects the curve at exactly one point, demonstrating that the cubic function passes the vertical line test and IS a function. For every x-value, there is exactly one corresponding y-value.

IS a function (passes vertical line test)

Example 1.3.1

Determine whether or not the relation represents $y$ as a function of $x$. Find the domain and range of those relations which are functions.

$\{(-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9)\}$

$\{(-3,0), (1,6), (2, -3), (4,2), (-5,6), (4, -9), (6,2)\}$

$\{(x, y) \, | \, x$ is an odd integer, and $y$ is an even integer$\}$

$\{(-2, y) \, | \, -3 < y < 4\}$

Example 1.3.2

Which of the following are functions of $x$ and why?

$x^2+y = 1$
$x + y^2 = 1$
$x + y^3 = 1$

Example 1.3.3

Find the domain and range of the function $y = \sqrt{x+8}$.

Example 1.3.4

Use the graph of $f(x)$ below to answer the questions about $f(x)$.

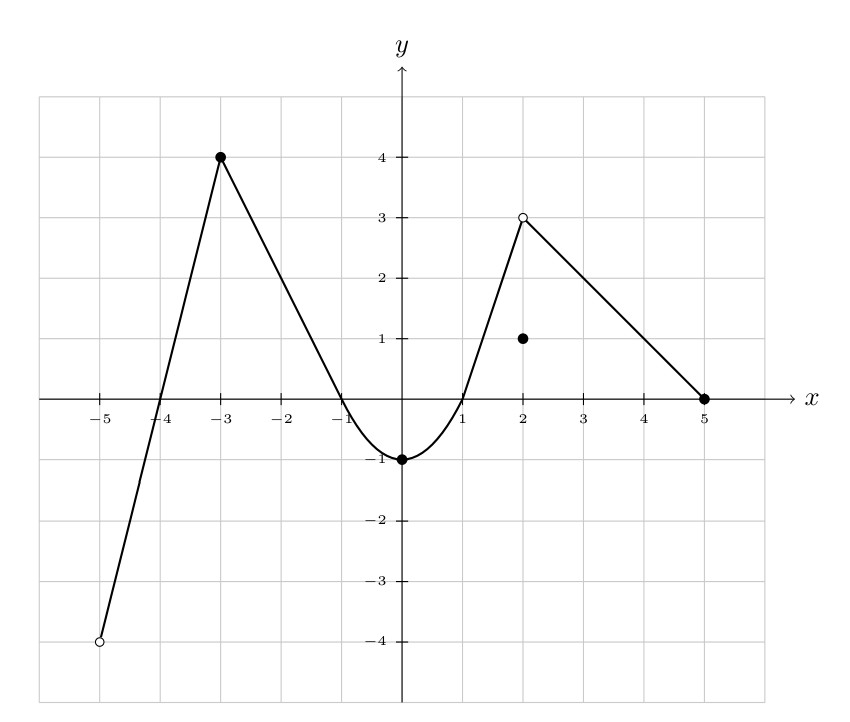
Piecewise function graph on a coordinate plane with gridlines ranging from approximately -7 to 8 on the x-axis and -4 to 5 on the y-axis. The graph consists of multiple line segments: starting from the left, there's a line segment with positive slope ending at an open circle around (-3, 5); a line segment with negative slope from a filled circle at (-3, 2) to an open circle around (2, 0); and a line segment with positive slope starting from a filled circle at (2, 1) extending to the right. The use of filled and open circles indicates whether endpoints are included or excluded in each piece of the piecewise function.

Find the domain of $f$.

Find the range of $f$.

Determine $f(2)$.

List the $x$-intercept(s), if any exist.

List the $y$-intercept(s), if any exist.

1.4 Function Notation

We can write a function several ways. The variable used to represent elements of the Domain is the independent variable and the variable used to represent elements of the Range is called the dependent variable. The most common way of writing a function is:

\[\underbrace{y}_{\substack{\text{dependent} \\ \text{variable}}} = f(\underbrace{x}_{\substack{\text{independent} \\ \text{variable}}}) = \underbrace{2x + 1}_{\text{rule}}\]

We can also write a function as:

\[f : x \rightarrow 2x+1\]

\[f : \{(x, y) \mid y = 2x+1 \}\]

Example 1.4.1

Consider the following function: $f(x) = 7x + 3$. Find the values of $f(0)$, $f(-1)$, $f(-1+h)$ and $f(x+h)$.

Example 1.4.2

Consider the following function: $f(x) = 4x^2 + 3x-22$. Find the values of $f(0)$, $f(-1)$, and $f(x+h)$.

Piecewise Functions

Example 1.4.3

Evaluate $f(0)$, $f(-1)$, $f(1)$, and $f(2)$ for:

\[f(x) = \begin{cases} x^2 + 2 & \text{if } x<1\\ 2x^2 +2 & \text{if } x \geq 1 \end{cases}\]

Example 1.4.4

Determine the domain for the function. Write your answer in Interval Notation and as an Inequality.

\[f(x)=-1+\sqrt{14x-5}\]

Example 1.4.5

Determine the domain for the function. Write your answer in Interval Notation and as an Inequality.

\[f(x) = \frac{3x+20}{x^2+8x-8}\]

Example 1.4.6

Let $g(s) = \frac{s}{s+1}-1$. Find the values of $g(10)$, $g\left(\frac{1}{11}\right)$, $g(-1/8)$

1.5 Function Arithmetic

Arithmetic Combinations

We can add, subtract, multiply and divide functions much like we do with real numbers.

Notation

$(f + g)(x) = f(x) + g(x)$
$(f - g)(x) = f(x) - g(x)$
$(f \cdot g)(x) = f(x) \cdot g(x)$
$\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}$

Example 1.5.1

If $f(x) = 2x + 3$ and $g(x) = x^2 +1$ find:

$(f + g)(x) = 2x +3 + x^2 + 1 = x^2 +2x +4$

$(f - g)(x) =$

$(f \cdot g)(x) =$

$\left(\frac{f}{g}\right)(x) =$

We can evaluate these new functions the exact same way we did before. Whatever is in the parentheses is replaced for $x$ in the equation.

Example 1.5.2

If $f(x) = x^2 +2x -3$ and $g(x) = x^3-3x^2 -4x$ find:

$(f + g)(-1) =$

$(f \cdot g)(2) =$

The domain of $\left(\frac{f}{g}\right)(x) =$

Example 1.5.3

Suppose $f(x) = x^2 -2x +1$. Find:

\[\frac{f(x+h)-f(x)}{h} \qquad \text{(Difference Quotient)}\]

Example 1.5.4

A company produces very unusual CD’s for which the variable cost is $7 per CD and the fixed costs are $30000. They will sell the CD’s for $52 each. Let $x$ be the number of CD’s produced.

Write the total cost $C$ as a function of the number of CD’s produced. $C(x)$
Write the total revenue $R$ as a function of the number of CD’s produced. $R(x)$
Write the total profit $P$ as a function of the number of CD’s produced. $P(x)$
Find the number of CD’s which must be produced to break even.

1.6 Graphs of Functions

Definition: The graph of a function $f$ is a collection of ordered pairs $(x, f(x))$ such that $x$ is in the domain of $f(x)$.

Recall:

$x$ is the distance in the $x$-direction. $y=f(x)$ is the distance in the $y$ direction.

Domain and Range

The domain of a function is those $x$-values that we can use in the function.

The range of a function is the $y$-values we get out of the function.

Example 1.6.1

$y= x^2$

Domain: All real numbers.

Range: $y \geq 0$.

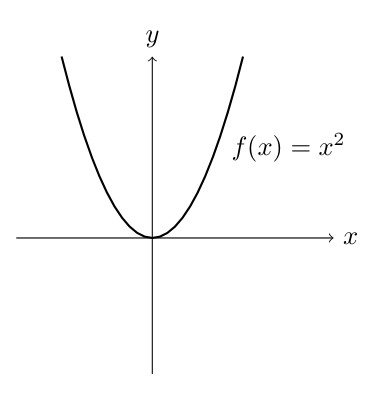
Graph of f(x) = x², the basic parabola. The parabola opens upward with vertex at the origin (0,0). The graph is symmetric about the y-axis and extends infinitely upward and outward on both sides. The domain is all real numbers and the range is y ≥ 0, showing that the function only produces non-negative output values.

Zeros of a Function

Definition: The zeros of a function $f(x)$ are those $x$-values for which $f(x) = 0$.

Q: How do we find the zeros of a function?

A: Set the function equal to zero. Also

Factor! Factor! Factor!

Example 1.6.2

Find the zeros of $f(x)=3x^2+22x-16$

Example 1.6.3

Find the zeros of $f(x) = \frac{x^2-9x+14}{4x}$.

Increasing and Decreasing Functions

Definition:

A function is increasing on an interval if for any $x_1$ and $x_2$ in the interval with $x_1 < x_2$ then $f(x_1) < f(x_2)$.

A function is decreasing on an interval if for any $x_1$ and $x_2$ in the interval with $x_1 < x_2$ then $f(x_1) > f(x_2)$.

A function is constant on an interval if for any $x_1$ and $x_2$ in the interval $f(x_1) = f(x_2)$.

Example 1.6.4

Graph of a decreasing cubic function showing a smooth curve that decreases from left to right across the entire visible domain. The function is continuously decreasing with no local maxima or minima.

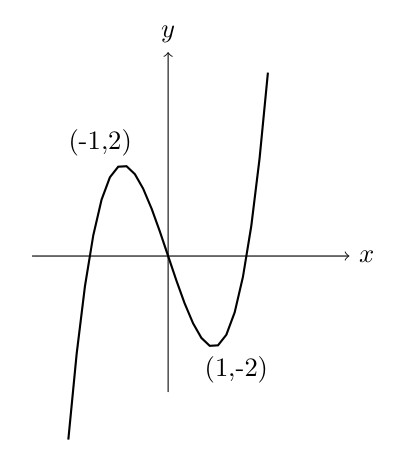
Graph of a cubic function f(x) = x³ with a local maximum and local minimum. The function decreases from left, reaches a local maximum, then decreases to a local minimum, and finally increases to the right. The curve shows two turning points, characteristic of a cubic polynomial.

Example 1.6.5

Use the graph to solve the equation $x^2+2x=0$

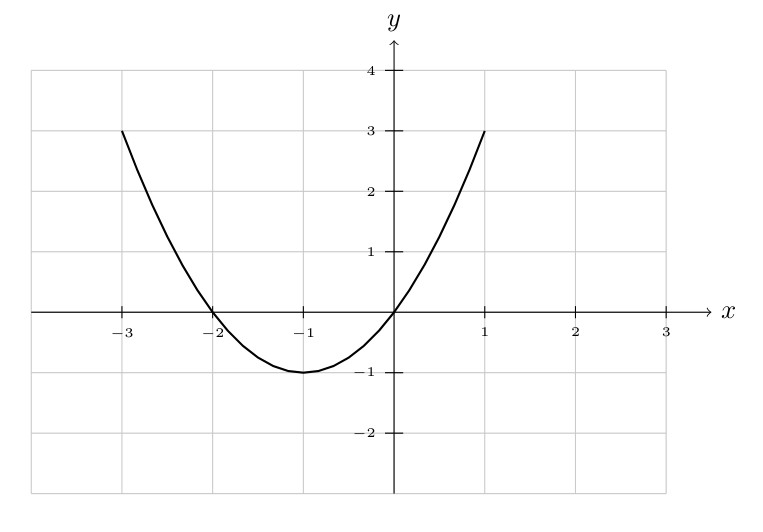
Graph of f(x) = x² + 2x, a parabola opening upward. The parabola crosses the x-axis at two points (the zeros of the function), has its vertex below the x-axis, and is used to solve the equation x² + 2x = 0 graphically by identifying where the curve intersects the x-axis.

Linear Functions

\[f(x) = mx +b \qquad \text{Linear Function}\]

Graph:

Example 1.6.6

Graph $f(x) = \frac{3}{2} x -2$

Step 1: Plot $y$-intercept.

Step 2: Plot another point using the slope $\frac{3}{2} = \frac{\text{rise}}{\text{run}}$

Empty coordinate grid for graphing linear functions

Graphing Piecewise Functions

Example 1.6.7

Graph:

\[f(x) = \begin{cases} \frac{3}{2}x - 2 & x \geq 2 \\ \\ \frac{3}{2}x + 7 & x < 2 \end{cases}\]

Example 1.6.8

Graph:

\[f(x) = \begin{cases} -x & x \leq 0 \\ 0 & 0 < x \leq 1 \\ x-1 & x >1 \end{cases}\]

Example 1.6.9

Write a piecewise function for the graph shown below.

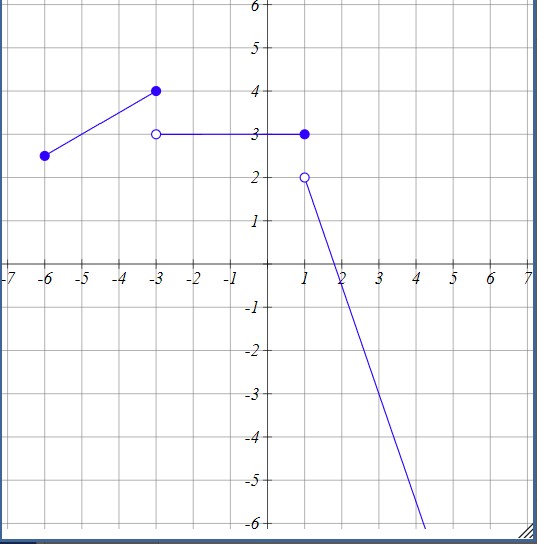
Piecewise function graph on a coordinate plane with grid from approximately -7 to 7 on the x-axis and 0 to 6 on the y-axis. The graph shows three distinct linear pieces: (1) a line segment with negative slope from approximately (-6, 3) to an open circle at approximately (-3, 3); (2) a horizontal line segment at y ≈ 3 from the filled circle at x ≈ -3 to a filled circle at approximately (1, 3); (3) a line segment with negative slope from the filled circle at (1, 3) extending down and to the right. The graph demonstrates a piecewise-defined function with three different linear pieces and uses open and filled circles to indicate whether endpoints are included.

Even and Odd Functions

Definition:

A function is even if $f(x) = f(-x)$ for all $x$ in the domain of $f(x)$.

A function is odd if $-f(x) = f(-x)$ for all $x$ in the domain of $f(x)$.

Example 1.6.10

Is $h(x) = x^5 - 5x^3$ even, odd or neither?

Look at $h(-x)$:

\[h(-x) = (-x)^5 -5(-x)^3\]

Example 1.6.11

Is $h(x) = x^4-3x^2$ even, odd or neither?

Look at $h(-x)$:

\[h(-x) = (-x)^4 - 3(-x)^2\]

Example 1.6.12

Is $h(x) = x^3 - 5$ even, odd or neither?

Look at $h(-x)$:

1.7 Transformations

Basic Graphs

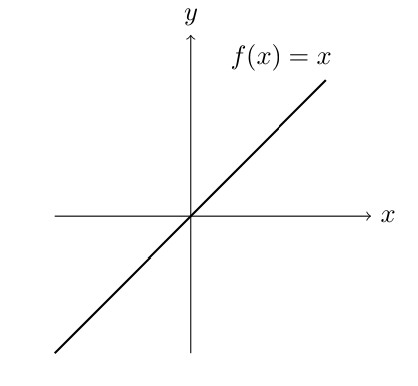
Graph of f(x) = x, the identity function, showing a straight line passing through the origin with slope 1, extending from lower left to upper right.

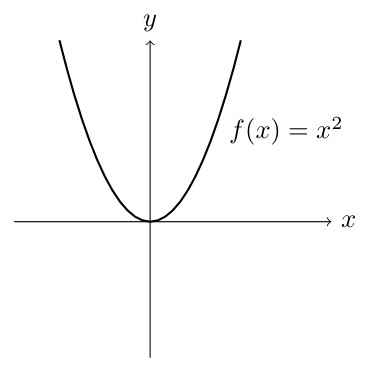
Graph of f(x) = x², the basic parabola, opening upward with vertex at the origin.

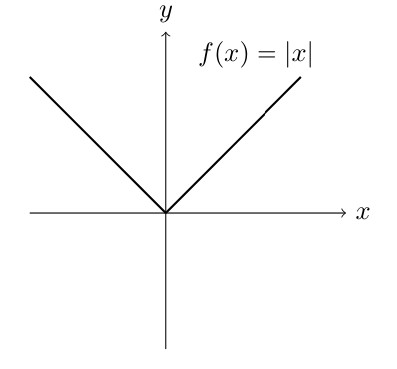
Graph of f(x) = |x|, the absolute value function, forming a V-shape with vertex at the origin.

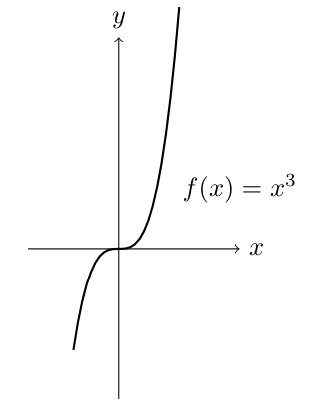
Graph of f(x) = x³, the cubic function, showing the characteristic S-shaped curve passing through the origin.

Shifting Graphs

Moving up and down

$h(x) =f(x) + a$ moves $f(x)$ up “$a$” units.

$h(x) =f(x) - a$ moves $f(x)$ down “$a$” units.

Example 1.7.1

$h(x)=x^3-3 = f(x) -3$ if $f(x) = x^3$. Graph $f(x)$ and $h(x)$ on the same set of axes.

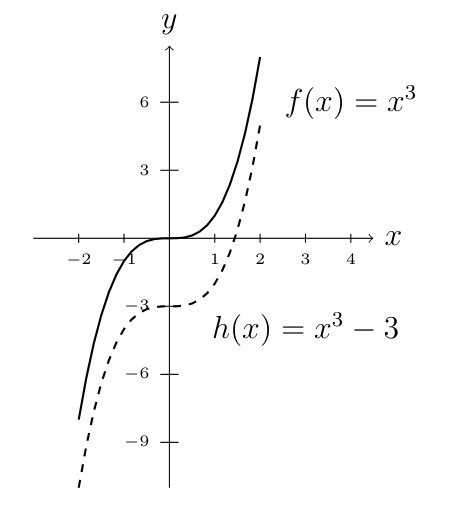
Graph showing f(x) = x³ (solid curve) and h(x) = x³ - 3 (dashed curve). The cubic function h(x) is the same shape as f(x) but shifted down 3 units. Both curves show the characteristic S-shape of cubic functions, with h(x) passing through (0, -3) instead of the origin.

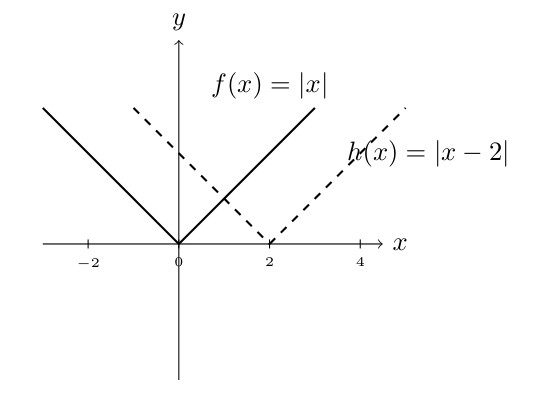
Moving left and right

$h(x) =f(x+a)$ moves $f(x)$ to the left “$a$” units.

$h(x) =f(x-a)$ moves $f(x)$ to the right “$a$” units.

Example 1.7.2

$h(x)=|x-2| = f(x-2)$ if $f(x) = |x|$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Graph showing f(x) = |x| (solid V-shape) and h(x) = |x-2| (dashed V-shape). The absolute value function h(x) has the same shape as f(x) but is shifted 2 units to the right, with its vertex at (2, 0) instead of the origin.

Example 1.7.3

$h(x)=(x+2)^3-3 = f(x+2)-3$ if $f(x) = x^3$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Large coordinate grid showing the transformation of a cubic function, with f(x) = x³ and h(x) = (x+2)³ - 3. The graph h(x) is shifted 2 units left and 3 units down from f(x).

Reflecting across $x$-axis

$h(x) =-f(x)$ reflects $f(x)$ across the $x$-axis.

Example 1.7.4

$h(x)=-x^2 = -f(x)$ if $f(x) = x^2$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Graph showing f(x) = x² (parabola opening upward) and h(x) = -x² (parabola opening downward). The function h(x) is the reflection of f(x) across the x-axis, both with vertex at the origin.

Example 1.7.5

$h(x)=-(x+2)^2+2 = -f(x+2)+2$ if $f(x) = x^2$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Graph showing f(x) = x² and h(x) = -(x+2)² + 2. The parabola h(x) is reflected across the x-axis (opening downward), shifted 2 units left, and shifted 2 units up, with vertex at (-2, 2).

Vertical stretch or expansion

\[h(x) =A \cdot f(x)\]

stretches $f(x)$ vertically if $A>1$ and expands $f(x)$ horizontally if $0<A<1$.

Example 1.7.6

$h(x)=2(x+3)^2-3 = 2f(x+3)-3$ where $f(x) = x^2$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Graph showing f(x) = x² and h(x) = 2(x+3)² - 3. The parabola h(x) is vertically stretched by a factor of 2, shifted 3 units left, and shifted 3 units down, with vertex at (-3, -3). The parabola h(x) is narrower (steeper) than f(x) due to the vertical stretch.

Given the function:

\[g(x) = A f(x + B) + C\]

the following transformations occur on $f(x)$:

$|A|$ stretches or expands the function $f(x)$ by a factor $|A|$.
$B$ moves the function $f(x)$ left ($B>0$) or right ($B<0$)
$C$ moves the function $f(x)$ up ($C>0$) or down ($C<0$)

A negative sign in front of the function ($A$ is negative) will reflect it over the $x$-axis.

Example 1.7.7

$h(x)=-\frac{1}{2}(x-4)^3+2 = -\frac{1}{2}f(x-4)+2$ if $f(x) = x^3$. Graph $f(x)$ and $h(x)$ on the same set of axes.

Graph showing f(x) = x³ and h(x) = -½(x-4)³ + 2. The cubic function h(x) is reflected across the x-axis, compressed vertically by a factor of ½, shifted 4 units right, and shifted 2 units up.

Example 1.7.8

Write the equations of the following graphs.

Coordinate grid showing a transformed parabola opening upward with vertex approximately at (0, -1), used as an exercise for students to write the equation based on the graph.

Example 1.7.9

Write the equations of the following graphs.

Coordinate grid showing two graphs: an upward V-shape (absolute value function transformation) in the upper portion with vertex around (0, 3), and a downward V-shape (reflected absolute value function) in the lower portion with vertex around (2, -2). Students must determine the equations for both transformed absolute value functions.

Example 1.7.10

Write the equation for the function that has the shape of $f(x)=x^2$ but is shifted 3 units to the left, 7 units up and then reflected across the $x$-axis.

Expression	Number Line
\(x > 2\)
\(x \geq 2\)
\(x \geq 2\) AND \(x \leq 4\)


\(x \leq 2\) OR \(x \geq 4\)


\(x \leq 2\) AND \(x \geq 4\)

Inequality notation	Inequality notation	Interval notation
\(x > 2\)		\((2, \infty)\)
\(x \geq 2\)		\([2, \infty)\)
\(x \geq 2\) AND \(x \leq 4\)	\(2 \leq x \leq 4\)	\([2, 4]\)
\(x \leq 2\) OR \(x \geq 4\)		\((-\infty, 2] \cup [4, \infty)\)

\(x\)	\(y=-2x+5\)
-1	\((-2)(-1)+5 = 7\)
0	\((-2)(0)+5 = 5\)
1	\((-2)(1)+5 = 3\)
2	\((-2)(2)+5 = 1\)
5/2	\((-2)(5/2)+5 = 0\)

Intercept	Description	How to Find
\(x\)-intercept	The point where the graph crosses the \(x\)-axis	Set \(y = 0\)
\(y\)-intercept	The point where the graph crosses the \(y\)-axis	Set \(x = 0\)

Symmetry	The equation is equivalent when…
\(y\)-axis	\(x\) is replaced with \(-x\)
\(x\)-axis	\(y\) is replaced with \(-y\)
origin	\(x\) and \(y\) are replaced by \(-x\) and \(-y\)